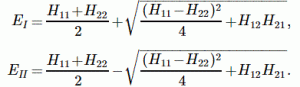I wrote a pretty abstract post on working with amplitudes, followed by more of the same, and then illustrated how it worked with a practical example (the ammonia molecule as a two-state system). Now it’s time for even more advanced stuff. Here we’ll show how to switch to another set of base states, and what it implies in terms of the Hamiltonian matrix and all of those equations, like those differential equations and – of course – the wavefunctions (or amplitudes) themselves. In short, don’t try to read this if you haven’t done your homework. 🙂
Let me continue the practical example, i.e. the example of the NH3 molecule, as shown below. We abstracted away from all of its motion, except for its angular momentum – or its spin, you’d like to say, but that’s rather confusing, because we shouldn’t be using that term for the classical situation we’re presenting here – around its axis of symmetry. That angular momentum doesn’t change from state | 1 〉 to state | 2 〉. What’s happening here is that we allow the nitrogen atom to flip through the other side, so it tunnels through the plane of the hydrogen atoms, thereby going through an energy barrier.
It’s important to note that we do not specify what that energy barrier consists of. In fact, the illustration above may be misleading, because it presents all sorts of things we don’t need right now, like the electric dipole moment, or the center of mass of the molecule, which actually doesn’t change, unlike what’s suggested above. We just put them there to remind you that (a) quantum physics is based on physics – so there’s lots of stuff involved – and (b) because we’ll need that electric dipole moment later. But, as we’re introducing it, note that we’re using the μ symbol for it, which is usually reserved for the magnetic dipole moment, which is what you’d usually associate when thinking about the angular momentum or the spin, both in classical as well as in quantum mechanics. So the direction of rotation of our molecule, as indicated by the arrow around the axis at the bottom, and the μ in the illustration itself, have nothing to do with each other. So now you know. Also, as we’re talking symbols, you should note the use of ε to represent an electric field. We’d usually write the electric dipole moment and the electric field vector as p and E respectively, but so we use that now for linear momentum and energy, and so we borrowed them from our study of magnets. 🙂
The point to note is that, when we’re talking about the ‘up’ or ‘down’ state of our ammonia molecule, you shouldn’t think of it as ‘spin up’ or ‘spin down’. It’s not like that: it’s just the nitrogen atom being beneath or above the plane of the hydrogen atoms, and we define beneath or above assuming the direction of spin actually stays the same!
OK. That should be clear enough. In quantum mechanics, the situation is analyzed by associating two energy levels with the ammonia molecule, E0 + A and E0 − A, so they are separated by an amount equal to 2A. This pair of energy levels has been confirmed experimentally: they are separated by an energy amount equal to 1×10−4 eV, so that’s less than a ten-thousandth of the energy of a photon in the visible-light spectrum. Therefore, a molecule that has a transition will emit a photon in the microwave range. The principle of a maser is based on exciting the the NH3 molecules, and then induce transitions. One can do that by applying an external electric field. The mechanism works pretty much like what we described when discussing the tunneling phenomenon: an external force field will change the energy factor in the wavefunction, by adding potential energy (let’s say an amount equal to U) to the total energy, which usually consists of the internal (Eint) and kinetic (p2/(2m) = m·v) energy only. So now we write a·e−i[(Eint + m·v + U)·t − p∙x]/ħ instead of a·e−i[(Eint + m·v)·t − p∙x]/ħ.
Of course, a·e−i·(E·t − p∙x)/ħ is an idealized wavefunction only, or a Platonic wavefunction – as I jokingly referred to it in my previous post. A real wavefunction has to deal with these uncertainties: we don’t know E and p. At best, we have a discrete set of possible values, like E0 + A and E0 − A in this case. But it might as well be some range, which we denote as ΔE and Δp, and then we need to make some assumption in regard to the probability density function that we’re going to associate with it. But I am getting ahead of myself here. Back to NH3, i.e. our simple two-state system. Let’s first do some mathematical gymnastics.
Choosing another representation
We have two base states in this system: ‘up’ or ‘down’, which we denoted as base state | 1 〉 and base state | 2 〉 respectively. You’ll also remember we wrote the amplitude to find the molecule in either one of these two states as:
- C1 = 〈 1 | ψ 〉 = (1/2)·e−(i/ħ)·(E0 − A)·t + (1/2)·e−(i/ħ)·(E0 + A)·t
- C2 = 〈 2 | ψ 〉 = (1/2)·e−(i/ħ)·(E0 − A)·t – (1/2)·e−(i/ħ)·(E0 + A)·t
That gave us the following probabilities:
If our molecule can be in two states only, and it starts off in one, then the probability that it will remain in that state will gradually decline, while the probability that it flips into the other state will gradually increase. So that’s what’s shown above, and it makes perfect sense.
Now, you may think there is only one possible set of base states here, as it’s not like measuring spin along this or that direction. These two base states are much simpler: it’s a matter of the nitrogen being beneath or above the plane of the hydrogens, and we’re only interested in the angular momentum of the molecule around its axis of symmetry to help us define what ‘up’ and what’s ‘down’. That’s all. However, from a quantum math point of view, we can actually choose some other ‘representation’. Now, these base state vectors | i 〉 are a bit tough to understand, so let’s, in our first go at it, use those coefficients Ci, which are ‘proper’ amplitudes. We’ll define two new coefficients, CI and CII, which – you’ve guess it – we’ll associate with an alternative set of base states | I 〉 and | II 〉. We’ll define them as follows:
- CI = 〈 I | ψ 〉 = (1/√2)·(C1 − C2)
- CII = 〈 II | ψ 〉 = (1/√2)·(C1 + C2)
[The (1/√2) factor is there because of the normalization condition, obviously. We could take it out and then do the whole analysis to plug it in later, as Feynman does, but I prefer to do it this way, as it reminds us that our wavefunctions are to be related to probabilities at some point in time. :-)]
Now, you can easily check that, when substituting our C1 and C2 for those wavefunctions above, we get:
- CI = 〈 I | ψ 〉 = (1/√2)·e−(i/ħ)·(E0 + A)·t
- CII = 〈 I | ψ 〉 = (1/√2)·e−(i/ħ)·(E0 − A)·t
Note that the way plus and minus signs switch here makes things not so easy to remember, but that’s how it is. 🙂 So we’ve got our stationary state solutions here, that are associated with probabilities that do not vary in time. [In case you wonder: that’s the definition of a ‘stationary state’: we’ve got something with a definite energy and, therefore, the probability that’s associated with it is some constant.] Of course, now you’ll cry wolf and say: these wavefunctions don’t actually mean anything, do they? They don’t describe how ammonia actually behaves, do they? Well… Yes and no. The base states I and II actually do allow us to describe whatever we need to describe. To be precise, describing the state φ in terms of the base states | 1 〉 and | 2 〉, i.e. writing | φ 〉 as:
| φ 〉 = | 1 〉 C1 + | 2 〉 C2,
is mathematically equivalent to writing:
| φ 〉 = | I 〉 CI + | II 〉 CII.
We can easily show that, even if it requires some gymnastics indeed—but then you should look at it as just another exercise in quantum math and so, yes, please do go through the logic. First note that the CI = 〈 I | ψ 〉 = (1/√2)·(C1 − C2) and CII = 〈 II | ψ 〉 = (1/√2)·(C1 + C2) expressions are equivalent to:
〈 I | ψ 〉 = (1/√2)·[〈 1 | ψ 〉 − 〈 2 | ψ 〉] and 〈 II | ψ 〉 = (1/√2)·[〈 1 | ψ 〉 + 〈 2 | ψ 〉]
Now, using our quantum math rules, we can abstract the | ψ 〉 away, and so we get:
〈 I | = (1/√2)·[〈 1 | − 〈 2 |] and 〈 II | = (1/√2)·[〈 1 | + 〈 2 |]
We could also have applied the complex conjugate rule to the expression for 〈 I | ψ 〉 above (the complex conjugate of a sum (or a product) is the sum (or the product) of the complex conjugates), and then abstract 〈 ψ | away, so as to write:
| I 〉 = (1/√2)·[| 1 〉 − | 2 〉] and | II 〉 = (1/√2)·[| 1 〉 + | 2 〉]
OK. So what? We’ve only shown our new base states can be written as similar combinations as those CI and CII coefficients. What proves they are base states? Well… The first rule of quantum math actually defines them as states i respecting the following condition:
〈 i | j〉 = 〈 j | i〉 = δij, with δij = δji is equal to 1 if i = j, and zero if i ≠ j
We can prove that as follows. First, use the | I 〉 = (1/√2)·[| 1 〉 − | 2 〉] and | II 〉 = (1/√2)·[| 1 〉 + | 2 〉] result above to check the following:
- 〈 I | I 〉 = (1/√2)·[〈 I | 1 〉 − 〈 I | 2 〉]
- 〈 II | II 〉 = (1/√2)·[〈 II | 1 〉 + 〈 II | 2 〉]
- 〈 II | I 〉 = (1/√2)·[〈 II | 1 〉 − 〈 II | 2 〉]
- 〈 I | II 〉 = (1/√2)·[〈 I | 1 〉 + 〈 I | 2 〉]
Now we need to find those 〈 I | i 〉 and 〈 II | i 〉 amplitudes. To do that, we can use that 〈 I | ψ 〉 = (1/√2)·[〈 1 | ψ 〉 − 〈 2 | ψ 〉] and 〈 II | ψ 〉 = (1/√2)·[〈 1 | ψ 〉 + 〈 2 | ψ 〉] equation and substitute:
- 〈 I | 1 〉 = (1/√2)·[〈 1 | 1 〉 − 〈 2 | 1 〉] = (1/√2)
- 〈 I | 2 〉 = (1/√2)·[〈 1 | 2 〉 − 〈 2 | 2 〉] = −(1/√2)
- 〈 II | 1 〉 = (1/√2)·[〈 1 | 1 〉 + 〈 2 | 1 〉] = (1/√2)
- 〈 II | 2 〉 = (1/√2)·[〈 1 | 2 〉 + 〈 2 | 2 〉] = (1/√2)
So we get:
- 〈 I | I 〉 = (1/√2)·[〈 I | 1 〉 − 〈 I | 2 〉] = (1/√2)·[(1/√2) + (1/√2)] = (2/(√2·√2) = 1
- 〈 II | II 〉 = (1/√2)·[〈 II | 1 〉 + 〈 II | 2 〉] = (1/√2)·[(1/√2) + (1/√2)] = 1
- 〈 II | I 〉 = (1/√2)·[〈 II | 1 〉 − 〈 II | 2 〉] = (1/√2)·[(1/√2) − (1/√2)] = 0
- 〈 I | II 〉 = (1/√2)·[〈 I | 1 〉 + 〈 I | 2 〉] = (1/√2)·[(1/√2) − (1/√2)] = 0
So… Well.. Yes. That’s equivalent to:
〈 I | I 〉 = 〈 II | II 〉 = 1 and 〈 I | II 〉 = 〈 II | I 〉 = 0
Therefore, we can confidently say that our | I 〉 = (1/√2)·[| 1 〉 − | 2 〉] and | II 〉 = (1/√2)·[| 1 〉 + | 2 〉] state vectors are, effectively, base vectors in their own right. Now, we’re going to have to grow very fond of matrices, so let me write our ‘definition’ of the new base vectors as a matrix formula:
You’ve seen this before. The two-by-two matrix is the transformation matrix for a rotation of state filtering apparatus about the y-axis, over an angle equal to (minus) 90 degrees, when only two states are involved:
You’ll wonder why we should go through all that trouble. Part of it, of course, is to just learn these tricks. The other reason, however, is that it does simplify calculations. Here I need to remind you of the Hamiltonian matrix and the set of differential equations that comes with it. For a system with two base states, we’d have the following set of equations:
Now, adding and subtracting those two equations, and then differentiating the expressions you get (with respect to t), should give you the following two equations:
So what about it? Well… If we transform to the new set of base states, and use the CI and CII coefficients instead of those C1 and C2 coefficients, then it turns out that our set of differential equations simplifies, because – as you can see – two out of the four Hamiltonian coefficients are zero, so we can write:
Now you might think that’s not worth the trouble but, of course, now you know how it goes, and so next time it will be easier. 🙂
On a more serious note, I hope you can appreciate the fact that with more states than just two, it will become important to diagonalize the Hamiltonian matrix so as simplify the problem of solving the related set of differential equations. Once we’ve got the solutions, we can always go back to calculate the wavefunctions we want, i.e. the C1 and C2 functions that we happen to like more in this particular case. Just to remind you of how this works, remember that we can describe any state φ both in terms of the base states | 1 〉 and | 2 〉 as well as in terms of the base states | I 〉 and | II 〉, so we can either write:
| φ 〉 = | 1 〉 C1 + | 2 〉 C2 or, alternatively, | φ 〉 = | I 〉 CI + | II 〉 CII.
Now, if we choose, or define, CI and CII the way we do – so that’s as CI = (1/√2)·(C1 − C2) and CII = (1/√2)·(C1 + C2) respectively – then the Hamiltonian matrices that come with them are the following ones:
To understand those matrices, let me remind you here of that equation for the Hamiltonian coefficients in those matrices:
Uij(t + Δt, t) = δij + Kij(t)·Δt = δij − (i/ħ)·Hij(t)·Δt
In my humble opinion, this makes the difference clear. The | I 〉 and | II 〉 base states are clearly separated, mathematically, as much as the | 1 〉 and | 2 〉 base states were separated conceptually. There is no amplitude to go from state I to state II, but then both states are a mix of state 1 and 2, so the physical reality they’re describing is exactly the same: we’re just pushing the temporal variation of the probabilities involved from the coefficients we’re using in our differential equations to the base states we use to define those coefficients – or vice versa.
Huh? Yes… I know it’s all quite deep, and I haven’t quite come to terms with it myself, so that’s why I’ll let you think about it. 🙂 To help you think this through, think about this: the C1 and C2 wavefunctions made sense but, at the same time, they were not very ‘physical’ (read: classical), because they incorporated uncertainty—as they mix two different energy levels. However, the associated base states – which I’ll call ‘up’ and ‘down’ here – made perfect sense, in a classical ‘physical’ sense, that is (my English seems to be getting poorer and poorer—sorry for that!). Indeed, in classical physics, the nitrogen atom is either here or there, right? Not somewhere in-between. 🙂 Now, the CI and CII wavefunctions make sense in the classical sense because they are stationary and, hence, they’re associated with a very definite energy level. In fact, as definite, or as classical, as when we say: the nitrogen atom is either here or there. Not somewhere in-between. But they don’t make sense in some other way: we know that the nitrogen atom will, sooner or later, effectively tunnel through. So they do not describe anything real. So how do we capture reality now? Our CI and CII wavefunctions don’t do that explicitly, but implicitly, as the base states now incorporate all of the uncertainty. Indeed, the CI and CII wavefunctions are described in terms of the base states I and II, which themselves are a mixture of our ‘classical’ up or down states. So, yes, we are kicking the ball around here, from a math point of view. Does that make sense? If not, sorry. I can’t do much more. You’ll just have to think through this yourself. 🙂
Let me just add one little note, totally unrelated to what I just wrote, to conclude this little excursion. I must assume that, in regard of diagonalization, you’ve heard about eigenvalues and eigenvectors. In fact, I must assume you heard about this when you learned about matrices in high school. So… Well… In case you wonder, that’s where we need this stuff. 🙂
OK. On to the next !
The general solution for a two-state system
Now, you’ll wonder why, after all of the talk about the need to simplify the Hamiltonian, I will now present a general solution for any two-state system, i.e. any pair of Hamiltonian equations for two-state systems. However, you’ll soon appreciate why, and you’ll also connect the dots with what I wrote above.
Let me first give you the general solution. In fact, I’ll copy it from Feynman (just click on it to enlarge it, or read it in Feynman’s Lecture on it yourself):
The problem is, of course, how do we interpret that solution? Let me make it big:
This says that the general solution to any two-state system amounts to calculating two separate energy levels using the Hamiltonian coefficients as they are being used in those equations above. So there is an ‘upper’ energy level, which is denoted as EI, and a ‘lower’ energy level, which is denoted as EII.
What? So it doesn’t say anything about the Hamiltonian coefficients themselves? No. It doesn’t. What did you expect? Those coefficients define the system as such. So the solution is as general as the ‘two-state system’ we wanted to solve: conceptually, it’s characterized by two different energy levels, but that’s about all we can say about it.
[…] Well… No. The solutions above are specific functional forms and, to find them, we had to make certain assumptions and impose certain conditions so as to ensure there’s any non-zero solution at all! In fact, that’s all the fine print above, so I won’t dwell on that—and you had better stop complaining! 🙂 Having said that, the solutions above are very general indeed, and so now it’s up to us to look at specific two-state systems, like our ammonia molecule, and make educated guesses so as to come up with plausible values or functional forms for those Hamiltonian coefficients. That’s what we did when we equated H11 and H22 with some average energy E0, and H12 and H12 with some energy A. [Minus A, in fact—but we might have chosen some positive value +A. Same solution. In fact, I wonder why Feynman didn’t go for the +A value. It doesn’t matter, really, because we’re talking energy differences, but… Well… Any case… That’s how it is. I guess he just wanted to avoid having to switch the indices 1 and 2, and the coefficients a and b and what have you. But it’s the same. Honestly. :-)]
So… Well… We could do the same here and analyze the solutions we’ve found in our previous posts but… Well… I don’t think that’s very interesting. In addition, I’ll make some references to that in my next post anyway, where we’re going to be analyzing the ammonia molecule in terms of it I and II states, so as to prepare a full-blown analysis of how a maser works.
Just to wet your appetite, let me tell you that the mysterious I and II states do have a wonderfully practical physical interpretation as well. Just scroll back it all the way up, and look at the opposite electric dipole moment that’s associated with state 1 and 2. Now, the two pictures have the angular momentum in the same direction, but we might expect that, when looking at a beam of random NH3 molecules – think of gas being let out of a little jet 🙂 – the angular momentum will be distributed randomly. So… Well… The thing is: the molecules in state I, or in state II, will all have their electric dipole moment lined up in the very same physical direction. So, in that sense, they’re really ‘up’ or ‘down’, and we’ll be able to separate them in an inhomogeneous electric field, just like we were able to separate ‘up’ or ‘down’ electrons, protons or whatever spin-1/2 particles in an inhomogeneous magnetic field.
But so that’s for the next post. I just wanted to tell you that our | I 〉 and | II 〉 base states do make sense. They’re more than just ‘mathematical’ states. They make sense as soon as we’re moving away from an analysis in terms of one NH3 molecule only because… Well… Are you surprised, really? You shouldn’t be. 🙂 Let’s go for it straight away.
The ammonia molecule in an electric field
Our educating guess of the Hamiltonian matrix for the ammonia molecule was the following:

This guess was ‘educated’ because we knew what we wanted to get out of it, and that’s those time-dependent probabilities to be in state 1 or state 2:
Now, we also know that state 1 and 2 are associated with opposite electric dipole moments, as illustrated below.
Hence, it’s only natural, when applying an external electric field ε to a whole bunch of ammonia molecules –think of some beam – that our ‘educated’ guess would change to:
Why the minus sign for με in the H22 term? You can answer that question yourself: the associated energy is μ·ε = μ·ε·cosθ, and θ is ±π here, as we’re talking opposite directions. So… There we are. 🙂 The consequences show when using those values in the general solution for our system of differential equations. Indeed, the
equations become:
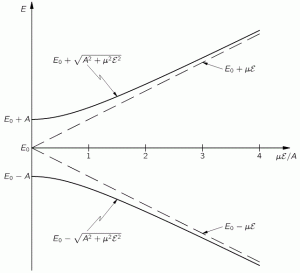
The graph of this looks as follows:
The upshot is: we can separate the the NH3 molecules in a inhomogeneous electric field based on their state, and then I mean state I or II, not state 1 or 2. How? Let me copy Feynman on that: it’s like a Stern-Gerlach apparatus, really. 🙂
 So that’s it. We get the following:
So that’s it. We get the following:
That will feed into the maser, which looks as follows:
But… Well… Analyzing how a maser works involves another realm of physics: cavities and resonances. I don’t want to get into that here. I only wanted to show you why and how different representations of the same thing are useful, and how it translates into a different Hamiltonian matrix. I think I’ve done that, and so let’s call it a night. 🙂 I hope you enjoyed this one. If not… Well… I did. 🙂
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:
https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 17, 2020 as a result of a DMCA takedown notice from Michael A. Gottlieb, Rudolf Pfeiffer, and The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 17, 2020 as a result of a DMCA takedown notice from Michael A. Gottlieb, Rudolf Pfeiffer, and The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 17, 2020 as a result of a DMCA takedown notice from Michael A. Gottlieb, Rudolf Pfeiffer, and The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 17, 2020 as a result of a DMCA takedown notice from Michael A. Gottlieb, Rudolf Pfeiffer, and The California Institute of Technology. You can learn more about the DMCA here: