In my two previous posts, I presented all of the ingredients of the meal we’re going to cook now, most notably:
- The formula for the torque on a loop of a current in a magnetic field, and its energy: (i) τ = μ×B, and (ii) Umech = −μ·B.
- The Biot-Savart Law, which gives you the magnetic field that’s produced by wires carrying currents:
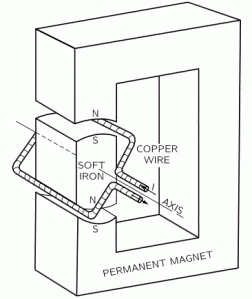
Both ingredients are, obviously, relevant to the design of an electromagnetic motor, i.e. an ‘engine that can do some work’, as Feynman calls it. 🙂 Its principle is illustrated below.
The two formulas above explain how and why the coil go around, and the coil can be made to keep going by arranging that the connections to the coil are reversed each half-turn by contacts mounted on the shaft. Then the torque is always in the same direction. That’s how a small direct current (DC) motor is made. My father made me make a couple of these thirty years ago, with a magnet, a big nail and some copper coil. I used sliding contacts, and they were the most difficult thing in the whole design. But now I found a very nice demo on YouTube of a guy whose system to ‘reverse’ the connections is wonderfully simple: he doesn’t use any sliding contacts. He just removes half of the insulation on the wire of the coil on one side. It works like a charm, but I think it’s not so sustainable, as it spins so fast that the insulation on the other side will probably come off after a while! 🙂
Now, to make this motor run, you need current and, hence, 19th century physicists and mechanical engineers also wondered how one could produce currents by changing the magnetic field. Indeed, they could use Alessandro Volta’s ‘voltaic pile‘ to produce currents but it was not very handy: it consisted of alternating zinc and copper discs, with pieces of cloth soaked in salt water in-between!
Now, while the Biot-Savart Law goes back to 1820, it took another decade to find out how that could be done. Initially, people thought magnetic fields should just cause some current, but that didn’t work. Finally, Faraday unequivocally established the fundamental principle that electric effects are only there when something is changing. So you’ll get a current in a wire by moving it in a magnetic field, or by moving the magnet or, if the magnetic field is caused by some other current, by changing the current in that wire. It’s referred to as the ‘flux rule’, or Faraday’s Law. Remember: we’ve seen Gauss’ Law, then Ampère’s Law, and then that Biot-Savart Law, and so now it’s time for Faraday’s Law. 🙂 Faraday’s Law is Maxwell’s third equation really, aka as the Maxwell-Faraday Law of Induction:
∇×E = −∂B/∂t
Now you’ll wonder: what’s flux got to do with this formula? ∇×E is about circulation, not about flux! Well… Let me copy Feynman’s answer:
So… There you go. And, yes, you’re right, instead of writing Faraday’s Law as ∇×E = −∂B/∂t, we should write it as:
That’s a easier to understand, and it’s also easier to work with, as we’ll see in a moment. So the point is: whenever the magnetic flux changes, there’s a push on the electrons in the wire. That push is referred to as the electromotive force, abbreviated as emf or EMF, and so it’s that line and/or surface integral above indeed. Let me paraphrase Feynman so you fully understand what we’re talking about here:
When we move our wire in a magnetic field, or when we move a magnet near the wire, or when we change the current in a nearby wire, there will be some net push on the electrons in the wire in one direction along the wire. There may be pushes in different directions at different places, but there will be more push in one direction than another. What counts is the push integrated around the complete circuit. We call this net integrated push the electromotive force (abbreviated emf) in the circuit. More precisely, the emf is defined as the tangential force per unit charge in the wire integrated over length, once around the complete circuit.
So that’s the integral. 🙂 And that’s how we can turn that motor above into a generator: instead of putting a current through the wire to make it turn, we can turn the loop, by hand or by a waterwheel or by whatever. Now, when the coil rotates, its wires will be moving in the magnetic field and so we will find an emf in the circuit of the coil, and so that’s how the motor becomes a generator.
Now, let me quickly interject something here: when I say ‘a push on the electrons in the wire’, what electrons are we talking about? How many? Well… I’ll answer that question in very much detail in a moment but, as for now, just note that the emf is some quantity expressed per coulomb or, as Feynman puts it above, per unit charge. So we’ll need to multiply it with the current in the circuit to get the power of our little generator.
OK. Let’s move on. Indeed, all I can do here is mention just a few basics, so we can move on to the next thing. If you really want to know all of the nitty-gritty, then you should just read Feynman’s Lecture on induced currents. That’s got everything. And, no, don’t worry: contrary to what you might expect, my ‘basics’ do not amount to a terrible pile of formulas. In fact, it’s all easy and quite amusing stuff, and I should probably include a lot more. But then… Well… I always need to move on… If not, I’ll never get to the stuff that I really want to understand. 😦
The electromotive force
We defined the electromotive force above, including its formula:
What are the units? Let’s see… We know B was measured not in newton per coulomb, like the electric field E, but in N·s/C·m, because we had to multiply the magnetic field strength with the velocity of the charge to find the force per unit charge, cf. the F/q = v×B equation. Now what’s the unit in which we’d express that surface integral? We must multiply with m2, so we get N·m·s/C. Now let’s simplify that by noting that one volt is equal to 1 N·m/C. [The volt has a number of definitions, but the one that applies here is that it’s the potential difference between two points that will impart one joule (i.e. 1 N·m) of energy to a unit of charge (i.e. 1 C) that passes between them.] So we can measure the magnetic flux in volt-seconds, i.e. V·s. And then we take the derivative in regard to time, so we divide by s, and so we get… Volt! The emf is measured in volt!
Does that make sense? I guess so: the emf causes a current, just like a potential difference, i.e. a voltage, and, therefore, we can and should look at the emf as a voltage too!
But let’s think about it some more, though. In differential form, Faraday’s Law, is just that ∇×E = −∂B/∂t equation, so that’s just one of Maxwell’s four equations, and so we prefer to write it as the “flux rule”. Now, the “flux rule” says that the electromotive force (abbreviated as emf or EMF) on the electrons in a closed circuit is equal to the time rate of change of the magnetic flux it encloses. As mentioned above, we measure magnetic flux in volt-seconds (i.e. V·s), so its time rate of change is measured in volt (because the time rate of change is a quantity expressed per second), and so the emf is measured in volt, i.e. joule per coulomb, as 1 V = 1 N·m/C = 1 J/C. What does it mean?
The time rate of change of the magnetic flux can change because the surface covered by our loop changes, or because the field itself changes, or by both. Whatever the cause, it will change the emf, or the voltage, and so it will make the electrons move. So let’s suppose we have some generator generating some emf. The emf can be used to do some work. We can charge a capacitor, for example. So how would that work?
More charge on the capacitor will increase the voltage V of the capacitor, i.e. the potential difference V = Φ1 − Φ2 between the two plates. Now, we know that the increase of the voltage V will be proportional to the increase of the charge Q, and that the constant of proportionality is defined by the capacity C of the capacitor: C = Q/V. [How do we know that? Well… Have a look at my post on capacitors.] Now, if our capacitor has an enormous capacity, then its voltage won’t increase very rapidly. However, it’s clear that, no matter how large the capacity, its voltage will increase. It’s just a matter of time. Now, its voltage cannot be higher than the emf provided by our ‘generator’, because it will then want to discharge through the same circuit!
So we’re talking power and energy here, and so we need to put some load on our generator. Power is the rate of doing work, so it’s the time rate of change of energy, and it’s expressed in joule per second. The energy of our capacitor is U = (1/2)·Q2/C = (1/2)·C·V2. [How do we know that? Well… Have a look at my post on capacitors once again. :-)] So let’s take the time derivative of U assuming some constant voltage V. We get: dU/dt = d[(1/2)·Q2/C]/dt = (Q/C)·dQ/dt = V·dQ/dt. So that’s the power that the generator would need to supply to charge the generator. As I’ll show in a moment, the power supplied by a generator is, indeed, equal to the emf times the current, and the current is the time rate of change of the charge, so I = dQ/dt.
So, yes, it all works out: the power that’s being supplied by our generator will be used to charge our capacitor. Now, you may wonder: what about the current? Where is the current in Faraday’s Law? The answer is: Faraday’s Law doesn’t have the current. It’s just not there. The emf is expressed in volt, and so that’s energy per coulomb, so it’s per unit charge. How much power an generator can and will deliver depends on its design, and the circuit and load that we will be putting on it. So we can’t say how many coulomb we will have. It all depends. But you can imagine that, if the loop would be bigger, or if we’d have a coil with many loops, then our generator would be able to produce more power, i.e. it would be able to move more electrons, so the mentioned power = (emf)×(current) product would be larger. 🙂
Finally, to conclude, note Feynman’s definition of the emf: the tangential force per unit charge in the wire integrated over length around the complete circuit. So we’ve got force times distance here, but per unit charge. Now, force times distance is work, or energy, and so… Yes, emf is joule per coulomb, definitely! 🙂
[…] Don’t worry too much if you don’t quite ‘get’ this. I’ll come back to it when discussing electric circuits, which I’ll do in my next posts.
Self-inductance and Lenz’s rule
We talked about motors and generators above. We also have transformers, like the one below. What’s going on here is that an alternating current (AC) produces a continuously varying magnetic field, which generates an alternating emf in the second coil, which produces enough power to light an electric bulb.
Now, the total emf in coil (b) is the sum of the emf’s of the separate turns of coil, so if we wind (b) with many turns, we’ll get a larger emf, so we can ‘transform’ the voltage to some other voltage. From your high-school classes, you should know how that works.
The thing I want to talk about here is something else, though. There is an induction effect in coil (a) itself. Indeed, the varying current in coil (a) produces a varying magnetic field inside itself, and the flux of this field is continually changing, so there is a self-induced emf in coil (a). The effect is called self-inductance, and so it’s the emf acting on a current itself when it is building up a magnetic field or, in general, when its field is changing in any way. It’s a most remarkable phenomenon, and so let me paraphrase Feynman as he describes it:
“When we gave “the flux rule” that the emf is equal to the rate of change of the flux linkage, we didn’t specify the direction of the emf. There is a simple rule, called Lenz’s rule, for figuring out which way the emf goes: the emf tries to oppose any flux change. That is, the direction of an induced emf is always such that if a current were to flow in the direction of the emf, it would produce a flux of B that opposes the change in B that produces the emf. In particular, if there is a changing current in a single coil (or in any wire), there is a “back” emf in the circuit. This emf acts on the charges flowing in the coil to oppose the change in magnetic field, and so in the direction to oppose the change in current. It tries to keep the current constant; it is opposite to the current when the current is increasing, and it is in the direction of the current when it is decreasing. A current in a self-inductance has “inertia,” because the inductive effects try to keep the flow constant, just as mechanical inertia tries to keep the velocity of an object constant.”
Hmm… That’s something you need to read a couple of times to fully digest it. There’s a nice demo on YouTube, showing an MIT physics video demonstrating this effect with a metal ring placed on the end of an electromagnet. You’ve probably seen it before: the electromagnet is connected to a current, and the ring flies into the air. The explanation is that the induced currents in the ring create a magnetic field opposing the change of field through it. So the ring and the coil repel just like two magnets with opposite poles. The effect is no longer there when a thin radial cut is made in the ring, because then there can be no current. The nice thing about the video is that it shows how the effect gets much more dramatic when an alternating current is applied, rather than a DC current. And it also shows what happens when you first cool the ring in liquid nitrogen. 🙂
You may also notice the sparks when the electromagnet is being turned on. Believe it or not, that’s also related to a “back emf”. Indeed, when we disconnect a large electromagnet by opening a switch, the current is supposed to immediately go to zero but, in trying to do so, it generates a large “back emf”: large enough to develop an arc across the opening contacts of the switch. The high voltage is also not good for the insulation of the coil, as it might damage it. So that’s why large electromagnets usually include some extra circuit, which allows the “back current” to discharge less dramatically. But I’ll refer you to Feynman for more details, as any illustration here would clutter the exposé.
Eddy currents
I like educational videos, and so I should give you a few references here, but there’s so many of this that I’ll let you google a few yourself. The most spectacular demonstration of eddy currents is those that appear in a superconductor: even back in the 1970s, when Feynman wrote his Lectures, the effect of magnetic levitation was well known. Feynman illustrates the effect with the simple diagram below: when bringing a magnet near to a perfect conductor, such as tin below 3.8°K, eddy currents will create opposing fields, so that no magnetic flux enters the superconducting material. The effect is also referred to as the Meisner effect, after the German physicist Walther Meisner, although it was discovered much earlier (in 1911) by a Dutch physicist in Leiden, Heike Kamerlingh Onnes, who got a Nobel Prize for it.
Of course, we have eddy currents in less dramatic situations as well. The phenomenon of eddy currents is usually demonstrated by the braking of a sheet of metal as it swings back and forth between the poles of an electromagnet, as illustrated below (left). The illustration on the right shows how eddy-current effect can be drastically reduced by cutting slots in the plate, so that’s like making a radial cut in our jumping ring. 🙂
The Faraday disc
The Faraday disc is interesting, not only from a historical point of view – the illustration below is a 19th century model, so Michael Faraday may have used himself – but also because it seems to contradict the “flux of rule”: as the disc rotates through a steady magnetic field, it will produce some emf, but so there’s no change in the flux. How is that possible?
The answer, of course, is that we are ‘cheating’ here: the material is moving, so we’re actually moving the ‘wire’, or the circuit if you want, so here we need to combine two equations:
If we do that, you’ll see it all makes sense. 🙂 Oh… That Faraday disc is referred to as a homopolar generator, and it’s quite interesting. You should check out what happened to the concept in the Wikipedia article on it. The Faraday disc was apparently used as a source for power pulses in the 1950s. The thing below could store 500 mega-joules and deliver currents up to 2 mega-ampère, i.e. 2 million amps! Fascinating, isn’t it? 🙂
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:
https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:









One thought on “Induced currents”