I did my last appearance on YouTube – Lecture X: have a look here !

I switched to AI and science fiction again, by reviving my turingtests.com blog. Last thing I did there goes back a decade. When I read it now, it was quite visionary. The post I did just now, is on space exploration. Enjoy !

🙂

You may think this is a rather poor joke: the spin of spin-1/2 particles must be 1/2, right?

Right. Yes. Let me ask you this: one half of what? What’s the unit here? And why would we take half of it?

If you are a somewhat informed reader, you’ll will be able to answer this: it’s a half-unit of Planck’s (reduced) quantum of action. It must be, right? Spin is expressed in units of ħ/2, isn’t it?

Right. Or not so bad as an answer, at least. Next question: if the Planck-Einstein relation tells us that physical action must come in full (not in half) units of h (we have no need for an E = hf/2 or E = hω/2 relation, do we?), then why would angular momentum (because that’s spin – orbital or spin angular momentum – if you express it in units of ħ or ħ/2, isn’t it?) come in half-units of ħ?

It is just one of those quantum-mechanical rules one cannot really understand, isn’t it? And so we should just accept it and go along with the rest of the story, isn’t it?

Well… No! We don’t agree. It’s not just one of those rules: we should understand what this is about. And the good news is this: we can. Moreover, it is actually not all that difficult. We’ve got the answers: check out the Matter page of this site.

Cheers – JL

Well… I think this is it, folks ! With my last posts on superconductivity, I think I am done. I’ve gone through all of the Lectures and it’s been a amazing adventure.

Looking back at it, I’d say: there is really no substitute for buying these Lectures yourself, and just grind through it. The only thing this blog really does is, perhaps, raise a question here and there – or help with figuring something out. But then… Well… If I can do it, you can do it. Don’t go for other sources if you can go for the original writings ! Read a classic rather than yet another second-hand or half-cooked thing !

I should also note that I started off using the print copy of Feynman’s Lectures but, at this point, I realize I should really acknowledge the incredible effort of two extraordinary people: Michael Gottlieb and Rudolf Pfeiffer, who have worked for decades to get those Lectures online. I borrowed a lot of stuff from it. In fact, in the coming weeks and months, I want to make sure I duly acknowledge that for all of the illustrations and quotes I’ve used, and if I haven’t been paraphrasing a bit too much, but… Well… That will be quite an effort. These two extraordinary guys also created a website for these Lectures which offers many more resources. That makes it accessible to all and everyone.

However, let me repeat: there is no substitute for buying the Lectures yourself, and grinding through it yourself. I wish you all the best on this journey. It’s been a nice journey for me, and I am therefore pretty sure you’ll enjoy it at least as much as I did.

Jean Louis Van Belle, 26 February 2018

Post scriptum: The material I have copied and republished from this wonderful online edition of Gottlieb and Pfeiffer is under copyright. The site mentions that, without explicit permission, only some limited copying is permitted under Fair Use laws, for non-commercial publications (which this blog surely is), and with proper attribution. I realize that, despite my best efforts to provide hyperlinks to the Lectures themselves whenever I’d borrow from them, I should probably go through it all to make sure that’s effectively the case. If I have been lacking in this regard, it was surely not intentional.

Pre-script (dated 26 June 2020): Our ideas have evolved into a full-blown realistic (or classical) interpretation of all things quantum-mechanical. In addition, I note the dark force has amused himself by removing some material. So no use to read this. Read my recent papers instead. 🙂

Original post:

This post is intended to help you think about, and work with, those mysterious amplitudes. More in particular, I’ll explore how potential differences change amplitudes. But let’s first recapitulate the basics.

In my previous post, I explained why the young French Comte Louis de Broglie, when writing his PhD thesis back in 1924, i.e. before Schrödinger, Born, Heisenberg and others had published their work, boldly proposed to the ω·t − k·x argument in the wavefunction of a particle with the relativistic invariant product of the momentum and position four-vectors p_μ = (E, p) = (E, p_x, p_y, p_z,) and x_μ = (t, x) = (t, x, y, z), provided the energy and momentum are re-scaled in terms of ħ. Hence, he wrote:

θ = ω·t − k·x = (p_μx_μ)/ħ = (E∙t − p∙x)/ħ = (E/ħ)∙t − (p/ħ)∙x

As it’s usually instructive to do a quick dimensional analysis, let’s do one here too. Energy is expressed in joule, and dividing it by the quantum of action, which is expressed in joule·seconds (J·s) gives us the dimension of an (angular) frequency indeed, which, in turns, yields a pure number. Likewise, linear momentum can be expressed in newton·seconds which, when divided by joule·seconds (J·s), yields a quantity expressed per meter. Hence, the dimension of p/ħ is m^–1, which again yields a pure number when multiplied with the dimension of the coordinates x, y or z.

In the mentioned post, I also gave an unambiguous answer to the question as to what energy concept should be used in the equation: it is the total energy of the particle we are trying to describe, so that includes its kinetic energy, its rest mass energy and, finally, its potential energy in whatever force field it may find itself, such as a gravitational and/or electromagnetic force field. Now, while we know that, when talking potential energy, we have some liberty in choosing the zero point of our energy scale, this issue is easily overcome by noting that we are always talking about the amplitude to go from one state to another, or to go from one point in spacetime to another. Hence, what matters is the potential difference, really.

Feynman, in his description of the conservation of energy in a quantum-mechanical context, distinguishes:

1. The rest energy m₀∙c², which he describes as the rest energy ‘of the parts of the particle’. [One should remember he wrote this before the existence of quarks and the associated theory of matter was confirmed.]
2. The energy ‘over and above’ the rest energy, which includes both the kinetic energy, i.e. m∙v²/2 = p²/(2m), as well as the ‘binding and/or excitation energy’, which he refers to as ‘internal energy’.
3. Finally, there is the potential energy, which we’ll denote by U.

In my previous post, I also gave you the relativistically correct formula for the energy of a particle with momentum p:

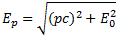
However, we will follow Feynman in his description, who uses the non-relativistic formula E_p = E_int + p²/(2m) + U. This is quite OK if we assume that the classical velocity of our particle does not approach the speed of light, so that covers a rather large number of real-life situations. Also, to make the example more real, we will assume the potential energy is electrostatic, and given by the formula U = q·Φ, with Φ the electrostatic potential (so just think of a number expressed in volt). Of course, q·Φ will be negative if the signs of q (i.e. the electric charge of our particle) and Φ are opposite, and positive if both have the same sign, as opposites attract and like repel when it comes to electric charge.

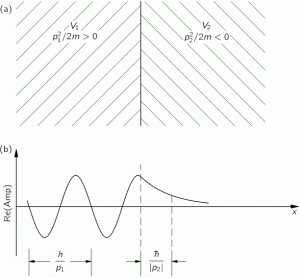
The illustration below visualizes the situation for Φ₂ < Φ₁. For example, we may assume Φ₁ is zero, that Φ₂ is negative, and that our particle is positively charged, so U₂ = qΦ₂ < 0. So it’s all rather simple really: we have two areas with a potential equal to U₁ = qΦ₁ and U₂ = qΦ₂ < 0 respectively. Hence, we need to use E₁ = E_int + p₁²/(2m) + U₁ to substitute ω₁ for E₁/ħ in the first area, and then E₂ = E_int + p₂²/(2m) + U₂ to substitute ω₂ for E₂/ħ in the second area, which U₂ – U₁ < 0.

The corresponding amplitudes, or wavefunctions, are:

1. Ψ₁(θ₁) = Ψ₁(x, t) = a·e^−iθ₁ = a·e^{−i[(E_int + p₁2/(2m) + U₁)·t − p₁∙x]/ħ} 
2. Ψ₂(θ₂) = Ψ₂(x, t) = a·e^−iθ₂ = a·e^{−i[(E_int + p₂2/(2m) + U₂)·t − p₂∙x]/ħ} 

Now how should we think about these two equations? We are definitely talking different wavefunctions. However, having said that, there is no reason to assume the different potentials would have an impact on the temporal frequency. Therefore, we can boldly equate ω₁ and ω₂ and, therefore, write that:

E_int + p₁²/(2m) + U₁ =  E_int + p₂²/(2m) + U₂ ⇔ p₁²/(2m) − p₂²/(2m) = U₂ – U₁ < 0

⇒ p₁² − p₂² < 0 ⇔ p₂ > p₁

What this says is that the kinetic energy, and/or the momentum, of our particle is greater in the second area, which is what we would classically expect, as a positive charged particle will pick up speed – and, therefore, momentum and kinetic energy – as it moves from an area with zero potential to an area with negative potential. However, the λ = h/p relation then implies that λ₂ = h/p₂ is smaller than λ₁ = h/p₂, which is what is illustrated by the dashed lines in the illustration above – which represent surfaces of equal phase, or wavefronts – and also by the second diagram in the illustration, which shows the real part of the complex-valued amplitude and compares the wavelengths λ₁ and λ₂. [As you know, the imaginary part is just like the real part but with a phase shift equal to π/2. Ideally, we should show both, but you get the idea.]

To sum it all up, the classical statement energy conservation principle is equivalent to the quantum-mechanical statement that the temporal frequency f or ω, i.e. the time-rate of change of the phase of the wavefunction, does not change – as long as the conditions do not change with time, of course – but that the spatial frequency, i.e. the wave number k or the wavelength λ – changes as the potential energy and/or kinetic energy change.

Tunneling

The p₁²/(2m) − p₂²/(2m) = U₂ – U₁ equation may be re-written to illustrate the quantum-mechanical effect of tunneling, i.e. the penetration of a potential barrier. Indeed, we can re-write p₁²/(2m) − p₂²/(2m) = U₂ – U₁ as

p₂² = 2m·[p₁²/(2m) − (U₂ – U₁)]

and, importantly, try to analyze what happens if U₂ – U₁ is larger than p₁²/(2m), so we get a negative value for p₂². Just imagine that Φ₁ is zero again, and that our particle is positively charged, but that Φ₂ is also positive (instead of negative, as in the example above), so our particle is being repelled. In practical terms, it means that our particle just doesn’t have enough energy to “climb the potential hill”. Quantum-mechanically, however, the amplitude is still given by that equation above, and we have a purely imaginary number for p₂, as the square root of a negative number is a purely imaginary number, just like √−4 = 2i. So let’s denote p₂ as i·p’ and let’s analyze what happens by breaking our a·e^iθ₂ function up in two separate parts by writing: a·e^−iθ₂ = a·e^{−i[(E₂/ħ)∙t − (i·p’/ħ)x]} = a·e^{−i(E₂/ħ)∙t}·e^{i2·p’·x/ħ} = a·e^{−i(E₂/ħ)∙t}·e^{−p’·x/ħ}.

Now, the e^{−p’·x/ħ} factor in our formula for a·e^−iθ₂ is a real-valued exponential function, and it’s a decreasing function, with the same shape as the general e^−x function, which I depict below.

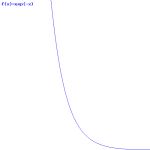
This e^{−p’·x/ħ} basically ‘kills’ our wavefunction as we move in the positive x-direction, past the potential barrier, which is what is illustrated below.

However, the story doesn’t finish here. We may imagine that the region with the prohibitive potential is rather small—like a few wavelengths only—and that, past that region, we’ve got another region where p₂² = 2m·[p₁²/(2m) − (U₂ – U₁)] is not negative. That’s the situation that’s depicted below, which also shows what might happen: the amplitude decays exponentially, but does not reach zero and, hence, there is a possibility that a particle might make it through the barrier, and that it will be found on the other side, with a real-valued and positive momentum and, hence, with a regular wavefunction.

Feynman gives a very interesting example of this: alpha-decay. Alpha decay is a type of radioactive decay in which an atomic nucleus emits an α-particle (so that’s a helium nucleus, really), thereby transforming or ‘decaying’ into an atom with a reduced mass and atomic number. The Wikipedia article on it hais not bad, but Feynman’s explanation is more to the point, especially when you’ve understood all of the above. The graph below illustrates the basic idea as it shows the potential energy U of an α-particle as a function of the distance from the center. As Feynman puts it: “If one tried to shoot an α-particle with the energy E into the nucleus, it would feel an electrostatic repulsion from the nucleus and would, classically, get no closer than the distance r₁, where its total energy is equal to U. Closer in, however, the potential energy is much lower because of the strong attraction of the short-range nuclear forces. How is it then that in radioactive decay we find α-particles which started out inside the nucleus coming out with the energy E? Because they start out with the energy E inside the nucleus and “leak” through the potential barrier.”

As for the numbers involved, the mean life of an α-particle in the uranium nucleus is as long as 4.5 billion years, according to Feynman, whereas the oscillations inside the nucleus are in the range of 10²² cycles per second! So how can one get a number like 10⁹ years from 10⁻²² seconds? The answer, as Feynman notes, is that that exponential gives a factor of about e⁻⁴⁵. So that gives the very small but definite probability of leakage. Once the α-particle is in the nucleus, there is almost no amplitude at all for finding it outside. However, if you take many nuclei and wait long enough, you’ll find one. 🙂

Now, that should be it for today, but let me end this post with something I should have told you a while ago, but then I didn’t, because I thought it would distract you from the essentials. If you’ve read my previous post carefully, you’ll note that I wrote the wavefunction as Ψ(θ) = a·e^iθ, rather as a·e^−iθ, with the minus sign in front of the complex exponent. So why is that?

There is a long and a short answer to that. I’ll give the short answer. You’ll remember that the phase of our wavefunction is like the hand of a stopwatch. Now we could imagine a stopwatch going counter-clockwise, and we could actually make one. Now, there is no arbitrariness here: it’s one way or the other, depending on our other conventions, and the phase of our complex-valued wavefunction does actually turn clockwise if we write things the way we’re writing them, rather than anti-clockwise. That’s a direction that’s actually not as per the usual mathematical convention: an angle in the unit circle is usually measured counter-clockwise. If you’d want it that way, we can fix easily by reversing the signs inside of the bracket, so we could write θ = k·x − ω·t, which is actually what you’ll often see. But so there’s only way to get it right: there’s a direction to it, and if we use the θ = ω·t − k·x, then we need the minus sign in the Ψ(θ) = a·e^−iθ equation.

It’s just one of those things that is easy to state, but actually gives us a lot of food for thought. Hence, I’ll probably come back to this one day. As for now, however, I think you’ve had enough. Or I’ve had enough, at least. 🙂 I hope this was not too difficult, and that you enjoyed it.

Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:

https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:

https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:

https://wordpress.com/support/copyright-and-the-dmca/