In our previous post, we talked a lot about symmetries in space – in a rather playful way. Let’s try to take it further here by doing some more thinking on symmetries in spacetime. This post will pick up some older stuff – from my posts on states and the related quantum math in November 2015, for example – but that shouldn’t trouble you too much. On the contrary, I actually hope to tie up some loose ends here.

Let’s first review some obvious ideas. Think about the direction of time. On a time axis, time goes from left to right. It will usually be measured from some zero point – like when we started our experiment or something 🙂 – to some +t point but we may also think of some point in time before our zero point, so the minus (−t) points – the left side of the axis – make sense as well. So the direction of time is clear and intuitive. Now, what does it mean to reverse the direction of time? We need to distinguish two things here: the convention, and… Well… Reality. If we would suddenly decide to reverse the direction in which we measure time, then that’s just another convention. We don’t change reality: trees and kids would still grow the way they always did. 🙂 We would just have to change the numbers on our clocks or, alternatively, the direction of rotation of the hand(s) of our clock, as shown below. [I only showed the hour hand because… Well… I don’t want to complicate things by introducing two time units. But adding the minute hand doesn’t make any difference.]

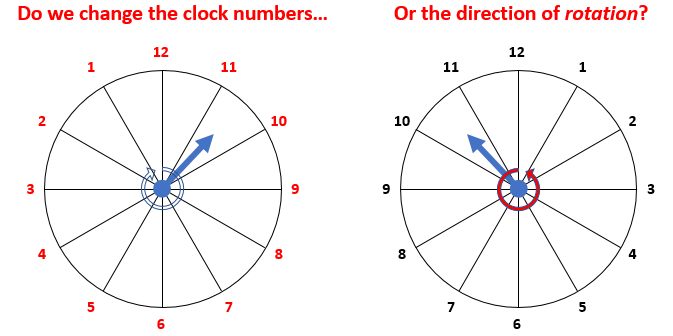Now, imagine you’re the dictator who decided to change our time measuring convention. How would you go about it? Would you change the numbers on the clock or the direction of rotation? Personally, I’d be in favor of changing the direction of rotation. Why? Well… First, we wouldn’t have to change expressions such as: “If you are looking north right now, then west is in the 9 o’clock direction, so go there.” 🙂 More importantly, it would align our clocks with the way we’re measuring angles. On the other hand, it would not align our clocks with the way the argument (θ) of our elementary wavefunction ψ = a·e^−iθ = e^{–i·(E·t – p·x)/ħ} is measured, because that’s… Well… Clockwise.

So… What are the implications here? We would need to change t for −t in our wavefunction as well, right? Yep. Good point. So that’s another convention that would change: we should write our elementary wavefunction now as ψ = a·e^{i·(E·t – p·x)/ħ}. So we would have to re-define θ as θ = –E·t + p·x = p·x –E·t. So… Well… Done!

So… Well… What’s next? Nothing. Note that we’re not changing reality here. We’re just adapting our formulas to a new dictatorial convention according to which we should count time from positive to negative – like 2, 1, 0, -1, -2 etcetera, as shown below. Fortunately, we can fix all of our laws and formulas in physics by swapping t for -t. So that’s great. No sweat.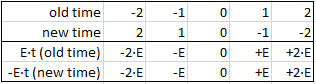 

Is that all? Yes. We don’t need to do anything else. We’ll still measure the argument of our wavefunction as an angle, so that’s… Well… After changing our convention, it’s now clockwise. 🙂 Whatever you want to call it: it’s still the same direction. Our dictator can’t change physical reality 🙂

Hmm… But so we are obviously interested in changing physical reality. I mean… Anyone can become a dictator, right? In contrast, we – enlightened scientists – want to really change the world, don’t we? 🙂 So what’s a time reversal in reality? Well… I don’t know… You tell me. 🙂 We may imagine some movie being played backwards, or trees and kids shrinking instead of growing, or some bird flying backwards – and I am not talking the hummingbird here. 🙂

Hey! The latter illustration – that bird flying backwards – is probably the better one: if we reverse the direction of time – in reality, that is – then we should also reverse all directions in space. But… Well… What does that mean, really? We need to think in terms of force fields here. A stone that’d be falling must now go back up. Two opposite charges that were going towards each other, should now move away from each other. But… My God! Such world cannot exist, can it?

No. It cannot. And we don’t need to invoke the second law of thermodynamics for that. 🙂 None of what happens in a movie that’s played backwards makes sense: a heavy stone does not suddenly fly up and decelerate upwards. So it is not like the anti-matter world we described in our previous post. No. We can effectively imagine some world in which all charges have been replaced by their opposite: we’d have positive electrons (positrons) around negatively charged nuclei consisting of antiprotons and antineutrons and, somehow, negative masses. But Coulomb’s law would still tell us two opposite charges – q₁ and –q₂ , for example – don’t repel but attract each other, with a force that’s proportional to the product of their charges, i.e. q₁·(-q₂) = –q₁·q₂. Likewise, Newton’s law of gravitation would still tell us that two masses m₁ and m₂ – negative or positive – will attract each other with a force that’s proportional to the product of their masses, i.e. m₁·m₂ = (-m₁)·(-m₂). If you’d make a movie in the antimatter world, it would look just like any other movie. It would definitely not look like a movie being played backwards.

In fact, the latter formula – m₁·m₂ = (-m₁)·(-m₂) – tells us why: we’re not changing anything by putting a minus sign in front of all of our variables, which are time (t), position (x), mass (m) and charge (q). [Did I forget one? I don’t think so.] Hence, the famous CPT Theorem – which tells us that a world in which (1) time is reversed, (2) all charges have been conjugated (i.e. all particles have been replaced by their antiparticles), and (3) all spatial coordinates now have the opposite sign, is entirely possible (because it would obey the same Laws of Nature that we, in our world, have discovered over the past few hundred years) – is actually nothing but a tautology. Now, I mean that literally: a tautology is a statement that is true by necessity or by virtue of its logical form. Well… That’s the case here: if we flip the signs of all of our variables, we basically just agreed to count or measure everything from positive to negative. That’s it. Full stop. Such exotic convention is… Well… Exotic, but it cannot change the real world. Full stop.

Of course, this leaves the more intriguing questions entirely open. Partial symmetries. Like time reversal only. 🙂 Or charge conjugation only. 🙂 So let’s think about that.

We know that the world that we see in a mirror must be made of anti-matter but, apart from that particularity, that world makes sense: if we drop a stone in front of the mirror, the stone in the mirror will drop down too. Two like charges will be seen as repelling each other in the mirror too, and concepts such as kinetic or potential energy look just the same. So time just seems to tick away in both worlds – no time reversal here! – and… Well… We’ve got two CP-symmetrical worlds here, don’t we? We only flipped the sign of the coordinate frame and of the charges. Both are possible, right? And what’s possible must exist, right? Well… Maybe. That’s the next step. Let’s first see if both are possible. 🙂

Now, when you’ve read my previous post, you’ll note that I did not flip the z-coordinate when reflecting my world in the mirror. That’s true. But… Well… That’s entirely beside the point. We could flip the z-axis too and so then we’d have a full parity inversion. [Or parity transformation – sounds more serious, doesn’t it? But it’s only a simple inversion, really.] It really doesn’t matter. The point is: axial vectors have the opposite sign in the mirror world, and so it’s not only about whether or not an antimatter world is possible (it should be, right?): it’s about whether or not the sign reversal of all of those axial vectors makes sense in each and every situation. The illustration below, for example, shows how a left-handed neutrino should be a right-handed antineutrino in the mirror world.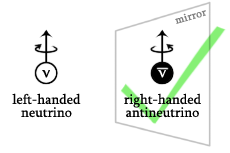I hope you understand the left- versus right-handed thing. Think, for example, of how the left-circularly polarized wavefunction below would look like in the mirror. Just apply the customary right-hand rule to determine the direction of the angular momentum vector. You’ll agree it will be right-circularly polarized in the mirror, right? That’s why we need the charge conjugation: think of the magnetic moment of a circulating charge! So… Well… I can’t dwell on this too much but – if Maxwell’s equations are to hold – then that world in the mirror must be made of antimatter.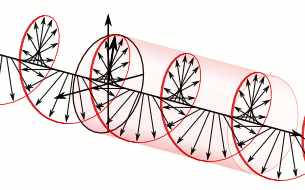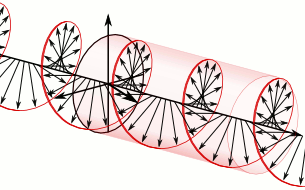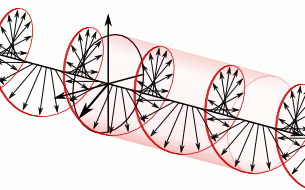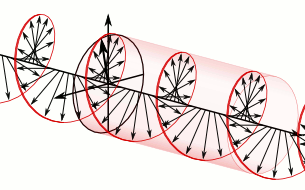

Now, we know that some processes – in our world – are not entirely CP-symmetrical. I wrote about this at length in previous posts, so I won’t dwell on these experiments here. The point is: these experiments – which are not easy to understand – lead physicists, philosophers, bloggers and what have you to solemnly state that the world in the mirror cannot really exist. And… Well… They’re right. However, I think their observations are beside the point. Literally.

So… Well… I would just like to make a very fundamental philosophical remark about all those discussions. My point is quite simple:

We should realize that the mirror world and our world are effectively separated by the mirror. So we should not be looking at stuff in the mirror from our perspective, because that perspective is well… Outside of the mirror. A different world. 🙂 In my humble opinion, the valid point of reference would be the observer in the mirror, like the photographer in the image below. Now note the following: if the real photographer, on this side of the mirror, would have a left-circularly polarized beam in front of him, then the imaginary photographer, on the other side of the mirror, would see the mirror image of this left-circularly polarized beam as a left-circularly polarized beam too. 🙂 I know that sounds complicated but re-read it a couple of times and – I hope – you’ll see the point. If you don’t… Well… Let me try to rephrase it: the point is that the observer in the mirror would be seeing our world – just the same laws and what have you, all makes sense! – but he would see our world in his world, so he’d see it in the mirror world. 🙂

Capito? If you would actually be living in the mirror world, then all the things you would see in the mirror world would make perfectly sense. But you would be living in the mirror world. You would not look at it from outside, i.e. from the other side of the mirror. In short, I actually think the mirror world does exist – but in the mirror only. 🙂 […] I am, obviously, joking here. Let me be explicit: our world is our world, and I think those CP violations in Nature are telling us that it’s the only real world. The other worlds exist in our mind only – or in some mirror. 🙂

Post scriptum: I know the Die Hard philosophers among you will now have an immediate rapid-backfire question. [Hey – I just invented a new word, didn’t I? A rapid-backfire question. Neat.] How would the photographer in the mirror look at our world? The answer to that question is simple: symmetry! He (or she) would think it’s a mirror world only. His world and our world would be separated by the same mirror. So… What are the implications here?

Well… That mirror is only a piece of glass with a coating. We made it. Or… Well… Some man-made company made it. 🙂 So… Well… If you think that observer in the mirror – I am talking about that image of the photographer in that picture above now – would actually exist, then… Well… Then you need to be aware of the consequences: the corollary of his existence is that you do not exist. 🙂 And… Well… No. I won’t say more. If you’re reading stuff like this, then you’re smart enough to figure it out for yourself. We live in one world. Quantum mechanics tells us the perspective on that world matters very much – amplitudes are different in different reference frames – but… Well… Quantum mechanics – or physics in general – does not give us many degrees of freedoms. None, really. It basically tells us the world we live in is the only world that’s possible, really. But… Then… Well… That’s just because physics… Well… When everything is said and done, it’s just mankind’s drive to ensure our perception of the Universe lines up with… Well… What we perceive it to be. 😦 or 🙂 Whatever your appreciation of it. Those Great Minds did an incredible job. 🙂