Post scriptum note added on 11 July 2016: This is one of the more speculative posts which led to my e-publication analyzing the wavefunction as an energy propagation. With the benefit of hindsight, I would recommend you to immediately the more recent exposé on the matter that is being presented here, which you can find by clicking on the provided link. In fact, I actually made some (small) mistakes when writing the post below.

Original post:

I’ve re-visited the de Broglie equations a couple of times already. In this post, however, I want to relate them to Schrödinger’s equation. Let’s start with the de Broglie equations first. Equations. Plural. Indeed, most popularizing books on quantum physics will give you only one of the two de Broglie equations—the one that associates a wavelength (λ) with the momentum (p) of a matter-particle:

λ = h/p

In fact, even the Wikipedia article on the ‘matter wave’ starts off like that and is, therefore, very confusing, because, for a good understanding of quantum physics, one needs to realize that the λ = h/p equality is just one of a pair of two ‘matter wave’ equations:

1. λ = h/p
2. f = E/h

These two equations give you the spatial and temporal frequency of the wavefunction respectively. Now, those two frequencies are related – and I’ll show you how in a minute – but they are not the same. It’s like space and time: they are related, but they are definitely not the same. Now, because any wavefunction is periodic, the argument of the wavefunction – which we’ll introduce shortly – will be some angle and, hence, we’ll want to express it in radians (or – if you’re really old-fashioned – degrees). So we’ll want to express the frequency as an angular frequency (i.e. in radians per second, rather than in cycles per second), and the wavelength as a wave number (i.e. in radians per meter). Hence, you’ll usually see the two de Broglie equations written as:

1. k = p/ħ
2. ω = E/ħ

It’s the same: ω = 2π∙f and f = 1/T (T is the period of the oscillation), and k = 2π/λ and then ħ = h/2π, of course! [Just to remove all ambiguities: stop thinking about degrees. They’re a Babylonian legacy, who thought the numbers 6, 12, and 60 had particular religious significance. So that’s why we have twelve-hour nights and twelve-hour days, with each hour divided into sixty minutes and each minute divided into sixty seconds, and – particularly relevant in this context – why ‘once around’ is divided into 6×60 = 360 degrees. Radians are the unit in which we should measure angles because… Well… Google it. They measure an angle in distance units. That makes things easier—a lot easier! Indeed, when studying physics, the last thing you want is artificial units, like degrees.]

So… Where were we? Oh… Yes. The de Broglie relation. Popular textbooks usually commit two sins. One is that they forget to say we have two de Broglie relations, and the other one is that the E = h∙f relationship is presented as the twin of the Planck-Einstein relation for photons, which relates the energy (E) of a photon to its frequency (ν): E = h∙ν = ħ∙ω. The former is criminal neglect, I feel. As for the latter… Well… It’s true and not true: it’s incomplete, I’d say, and, therefore, also very confusing.

Why? Because both things lead one to try to relate the two equations, as momentum and energy are obviously related. In fact, I’ve wasted days, if not weeks, on this. How are they related? What formula should we use? To answer that question, we need to answer another one: what energy concept should we use? Potential energy? Kinetic energy? Should we include the equivalent energy of the rest mass?

One quickly gets into trouble here. For example, one can try the kinetic energy, K.E. = m∙v²/2, and use the definition of momentum (p = m∙v), to write E = p²/(2m), and then we could relate the frequency f to the wavelength λ using the general rule that the traveling speed of a wave is equal to the product of its wavelength and its frequency (v = λ∙f). But if E = p²/(2m) and f = v/λ, we get:

p²/(2m) = h∙v/λ ⇔  λ = 2∙h/p

So that is almost right, but not quite: that factor 2 should not be there. In fact, it’s easy to see that we’d get de Broglie’s λ = h/p equation from his E = h∙f equation if we’d use E = m∙v² rather than E = m∙v²/2. In fact, the E = m∙v² relation comes out of them if we just multiply the two and, yes, use that v = f·λ relation once again:

1. f·λ = (E/h)·(h/p) = E/p
2. v = f·λ ⇒ f·λ = v = E/p ⇔ E = v·p = v·(m·v) ⇒ E = m·v²

But… Well… E = m∙v²? How could we possibly justify the use of that formula?

The answer is simple: our v = f·λ equation is wrong. It’s just something one shouldn’t apply to the complex-valued wavefunction. The ‘correct’ velocity formula for the complex-valued wavefunction should have that 1/2 factor, so we’d write 2·f·λ = v to make things come out alright. But where would this formula come from?

Well… Now it’s time to introduce the wavefunction.

The wavefunction

You know the elementary wavefunction:

ψ = ψ(x, t) = e^{−i(ωt − kx)} = e^{i(kx − ωt)} = cos(kx−ωt) + i∙sin(kx−ωt)

As for terminology, note that the term ‘wavefunction’ refers to what I write above, while the term ‘wave equation’ usually refers to Schrödinger’s equation, which I’ll introduce in a minute. Also note the use of boldface indicates we’re talking vectors, so we’re multiplying the wavenumber vector k with the position vector x = (x, y, z) here, although we’ll often simplify and assume one-dimensional space. In any case…

So the question is: why can’t we use the v = f·λ formula for this wave? The period of cosθ + isinθ is the same as that of the sine and cosine function considered separately: cos(θ+2π) + isin(θ+2π) = cosθ + isinθ, so T = 2π and f = 1/T = 1/2π do not change. So the f, T and λ should be the same, no?

No. We’ve got two oscillations for the price of one here: one ‘real’ and one ‘imaginary’—but both are equally essential and, hence, equally ‘real’. So we’re actually combining two waves. So it’s just like adding other waves: when adding waves, one gets a composite wave that has (a) a phase velocity and (b) a group velocity.

Huh? Yes. It’s quite interesting. When adding waves, we usually have a different ω and k for each of the component waves, and the phase and group velocity will depend on the relation between those ω’s and k’s. That relation is referred to as the dispersion relation. To be precise, if you’re adding waves, then the phase velocity of the composite wave will be equal to v_p = ω/k, and its group velocity will be equal to v_g = dω/dk. We’ll usually be interested in the group velocity, and so to calculate that derivative, we need to express ω as a function of k, of course, so we write ω as some function of k, i.e. ω = ω(k). There are number of possibilities then:

1. ω and k may be directly proportional, so we can write ω as ω = a∙k: in that case, we find that v_p = v_g = a.
2. ω and k are not directly proportional but have a linear relationship, so we can write write ω as ω = a∙k + b. In that case, we find that v_g = a and… Well… We’ve got a problem calculating v_p, because we don’t know what k to use!
3. ω and k may be non-linearly related, in which case… Well… One does has to do the calculation and see what comes out. 🙂

Let’s now look back at our e^{i(kx − ωt)} = cos(kx−ωt) + i∙sin(kx−ωt) function. You’ll say that we’ve got only one ω and one k here, so we’re not adding waves with different ω’s and k’s. So… Well… What?

That’s where the de Broglie equations come in. Look: k = p/ħ, and ω = E/ħ. If we now use the correct energy formula, i.e. the kinetic energy formula E = m·v²/2 (rather than that nonsensical E = m·v² equation) – which we can also write as E = m·v·v/2 = p·v/2 = p·p/2m = p²/2m, with v = p/m the classical velocity of the elementary particle that Louis de Broglie was thinking of – then we can calculate the group velocity of our e^{i(kx − ωt)} = cos(kx−ωt) + i∙sin(kx−ωt) as:

v_g = dω/dk = d[E/ħ]/d[p/ħ] = dE/dp = d[p²/2m]/dp = 2p/2m = p/m = v

However, the phase velocity of our e^{i(kx − ωt)} is:

v_p = ω/k = (E/ħ)/(p/ħ) = E/p = (p²/2m)/p = p/2m = v/2

So that factor 1/2 only appears for the phase velocity. Weird, isn’t it? We find that the group velocity (v_g) of the e^{i(kx − ωt)} function is equal to the classical velocity of our particle (i.e. v), but that its phase velocity (v_p) is equal to v divided by 2.

Hmm… What to say? Well… Nothing much—except that it makes sense, and very much so, because it’s the group velocity of the wavefunction that’s associated with the classical velocity of a particle, not the phase velocity. In fact, if we include the rest mass in our energy formula, so if we’d use the relativistic E = γm₀c² and p = γm₀v formulas (with γ the Lorentz factor), then we find that v_p = ω/k = E/p = (γm₀c²)/(γm₀v) = c²/v, and so that’s a superluminal velocity, because v is always smaller than c!

What? That’s even weirder! If we take the kinetic energy only, we find a phase velocity equal to v/2, but if we include the rest energy, then we get a superluminal phase velocity. It must be one or the other, no? Yep! You’re right! So that makes us wonder: is E = m·v²/2 really the right energy concept to use? The answer is unambiguous: no! It isn’t! And, just for the record, our young nobleman didn’t use the kinetic energy formula when he postulated his equations in his now famous PhD thesis.

So what did he use then? Where did he get his equations?

I am not sure. 🙂 A stroke of genius, it seems. According to Feynman, that’s how Schrödinger got his equation too: intuition, brilliance. In short, a stroke of genius. 🙂 Let’s relate these these two gems.

Schrödinger’s equation and the two de Broglie relations

Erwin Schrödinger and Louis de Broglie published their equations in 1924 and 1926 respectively. Can they be related? The answer is: yes—of course! Let’s first look at de Broglie‘s energy concept, however. Louis de Broglie was very familiar with Einsteins’ work and, hence, he knew that the energy of a particle consisted of three parts:

1. The particle’s rest energy m₀c², which de Broglie referred to as internal energy (E_int): this ‘internal energy’ includes the rest mass of the ‘internal pieces’, as he put it (now we call those ‘internal pieces’ quarks), as well as their binding energy (i.e. the quarks’interaction energy);
2. Any potential energy it may have because of some field (so de Broglie was not assuming the particle was traveling in free space), which we’ll denote by V: the field(s) can be anything—gravitational, electromagnetic—you name it: whatever changes the energy because of the position of the particle;
3. The particle’s kinetic energy, which we wrote in terms of its momentum p: K.E. = m·v²/2 = m²·v²/(2m) = (m·v)²/(2m) = p²/(2m).

Indeed, in my previous posts, I would write the wavefunction as de Broglie wrote it, which is as follows:

ψ(θ) = ψ(x, t) = a·e^−iθ = a·e^{−i[(E_int + p2/(2m) + V)·t − p∙x]/ħ} 

In those post – such as my post on virtual particles – I’d also note how a change in potential energy plays out: a change in potential energy, when moving from one place to another, would change the wavefunction, but through the momentum only—so it would impact the spatial frequency only. So the change in potential would not change the temporal frequencies ω₁ = E_int + p₁²/(2m) + V₁ and ω₁ = E_int + p₂²/(2m) + V₂. Why? Or why not, I should say? Because of the energy conservation principle—or its equivalent in quantum mechanics. The temporal frequency f or ω, i.e. the time-rate of change of the phase of the wavefunction, does not change: all of the change in potential, and the corresponding change in kinetic energy, goes into changing the spatial frequency, i.e. the wave number k or the wavelength λ, as potential energy becomes kinetic or vice versa.

So is that consistent with what we wrote above, that E = m·v²? Maybe. Let’s think about it. Let’s first look at Schrödinger’s equation in free space (i.e. a space with zero potential) once again:

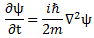
If we insert our ψ = e^{i(kx − ωt)} formula in Schrödinger’s free-space equation, we get the following nice result. [To keep things simple, we’re just assuming one-dimensional space for the calculations, so ∇²ψ = ∂²ψ/∂x². But the result can easily be generalized.] The time derivative on the left-hand side is ∂ψ/∂t = −iω·e^{i(kx − ωt)}. The second-order derivative on the right-hand side is ∂²ψ/∂x² = (ik)·(ik)·e^{i(kx − ωt)} = −k²·e^{i(kx − ωt)} . The e^{i(kx − ωt)} factor on both sides cancels out and, hence, equating both sides gives us the following condition:

−iω = −(iħ/2m)·k² ⇔ ω = (ħ/2m)·k²

Substituting ω = E/ħ and k = p/ħ yields:

E/ħ = (ħ/2m)·p²/ħ² = m²·v²/(2m·ħ) = m·v²/(2ħ) ⇔ E = m·v²/2

Bingo! We get that kinetic energy formula! But now… What if we’d not be considering free space? In other words: what if there is some potential? Well… We’d use the complete Schrödinger equation, which is:

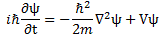
Huh? Why is there a minus sign now? Look carefully: I moved the iħ factor on the left-hand side to the other when writing the free space version. If we’d do that for the complete equation, we’d get:

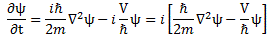I like that representation a lot more—if only because it makes it a lot easier to interpret the equation—but, for some reason I don’t quite understand, you won’t find it like that in textbooks. Now how does it work when using the complete equation, so we add the −(i/ħ)·V·ψ term? It’s simple: the e^{i(kx − ωt)} factor also cancels out, and so we get:

−iω = −(iħ/2m)·k²−(i/ħ)·V ⇔ ω = (ħ/2m)·k² + V/ħ

Substituting ω = E/ħ and k = p/ħ once more now yields:

E/ħ = (ħ/2m)·p²/ħ² + V/ħ = m²·v²/(2m·ħ) + V/ħ = m·v²/(2ħ) + V/ħ ⇔ E = m·v²/2 + V

Bingo once more!

The only thing that’s missing now is the particle’s rest energy m₀c², which de Broglie referred to as internal energy (E_int). That includes everything, i.e. not only the rest mass of the ‘internal pieces’ (as said, now we call those ‘internal pieces’ quarks) but also their binding energy (i.e. the quarks’interaction energy). So how do we get that energy concept out of Schrödinger’s equation? There’s only one answer to that: that energy is just like V. We can, quite simply, just add it.

That brings us to the last and final question: what about our v_g = v result if we do not use the kinetic energy concept, but the E = m·v²/2 + V + E_int concept? The answer is simple: nothing. We still get the same, because we’re taking a derivative and the V and E_int just appear as constants, and so their derivative with respect to p is zero. Check it:

v_g = dω/dk = d[E/ħ]/d[p/ħ] = dE/dp = d[p²/2m + V + E_int ]/dp = 2p/2m = p/m = v

It’s now pretty clear how this thing works. To localize our particle, we just superimpose a zillion of these e^{−i(ωt − kx)} equations. The only condition is that we’ve got that fixed v_g = dω/dk = v relationhip, but so we do have such fixed relationship—as you can see above. In fact, the Wikipedia article on the dispersion relation mentions that the de Broglie equations imply the following relation between ω and k: ω = ħk²/2m. As you can see, that’s not entirely correct: the author conveniently forgets the potential (V) and the rest energy (E_int) in the energy formula here!

What about the phase velocity? That’s a different story altogether. You can think about that for yourself. 🙂

I should make one final point here. As said, in order to localize a particle (or, to be precise, its wavefunction), we’re going to add a zillion elementary wavefunctions, each of which will make its own contribution to the composite wave. That contribution is captured by some coefficient a_i in front of every e^−iθ_i function, so we’ll have a zillion a_ie^−iθ_i functions, really. [Yep. Bit confusing: I use i here as subscript, as well as imaginary unit.] In case you wonder how that works out with Schrödinger’s equation, the answer is – once again – very simple: both the time derivative (which is just a first-order derivative) and the Laplacian are linear operators, so Schrödinger’s equation, for a composite wave, can just be re-written as the sum of a zillion ‘elementary’ wave equations.

So… Well… We’re all set now to effectively use Schrödinger’s equation to calculate the orbitals for a hydrogen atom, which is what we’ll do in our next post.

In the meanwhile, you can amuse yourself with reading a nice Wikibook article on the Laplacian, which gives you a nice feel for what Schrödinger’s equation actually represents—even if I gave you a good feel for that too on my Essentials page. Whatever. You choose. Just let me know what you liked best. 🙂

Oh… One more point: the v_g = dω/dk = d[p²/2m]/dp = p/m = v calculation obviously assumes we can treat m as a constant. In fact, what we’re actually doing is a rather complicated substitution of variables: you should write it all out—but that’s not the point here. The point is that we’re actually doing a non-relativistic calculation. Now, that does not mean that the wavefunction isn’t consistent with special relativity. It is. In fact, in one of my posts, I show how we can explain relativistic length contraction using the wavefunction. But it does mean that our calculation of the group velocity is not relativistically correct. But that’s a minor point: I’ll leave it for you as an exercise to calculate the relativistically correct formula for the group velocity. Have fun with it! 🙂

Note: Notations are often quite confusing. One should, generally speaking, denote a frequency by ν (nu), rather than by f, so as to not cause confusion with any function f, but then… Well… You create a new problem when you do that, because that Greek letter nu (ν) looks damn similar to the v of velocity, so that’s why I’ll often use f when I should be using nu (ν). As for the units, a frequency is expressed in cycles per second, while the angular frequency ω is expressed in radians per second. One cycle covers 2π radians and, therefore, we can write: ν = ω/2π. Hence, h∙ν = h∙ω/2π = ħ∙ω. Both ν as well as ω measure the time-rate of change of the phase of the wave function, as opposed to k, i.e. the spatial frequency of the wave function, which depends on the speed of the wave. Physicists also often use the symbol v for the speed of a wave, which is also hugely confusing, because it’s also used to denote the classical velocity of the particle. And then there’s two wave velocities, of course: the group versus the phase velocity. In any case… I find the use of that other symbol (c) for the wave velocity even more confusing, because this symbol is also used for the speed of light, and the speed of a wave is not necessarily (read: usually not) equal to the speed of light. In fact, both the group as well as the phase velocity of a particle wave are very different from the speed of light. The speed of a wave and the speed of light only coincide for electromagnetic waves and, even then, it should be noted that photons also have amplitudes to travel faster or slower than the speed of light.