Pre-script (dated 26 June 2020): Our ideas have evolved into a full-blown realistic (or classical) interpretation of all things quantum-mechanical. In addition, I note the dark force has amused himself by removing some material. So no use to read this. Read my recent papers instead. 🙂
Original post:
We are going to venture beyond quantum mechanics as it is usually understood – covering electromagnetic interactions only. Indeed, all of my posts so far – a bit less than 200, I think 🙂 – were all centered around electromagnetic interactions – with the model of the hydrogen atom as our most precious gem, so to speak.
In this post, we’ll be talking the strong force – perhaps not for the first time but surely for the first time at this level of detail. It’s an entirely different world – as I mentioned in one of my very first posts in this blog. Let me quote what I wrote there:
“The math describing the ‘reality’ of electrons and photons (i.e. quantum mechanics and quantum electrodynamics), as complicated as it is, becomes even more complicated – and, important to note, also much less accurate – when it is used to try to describe the behavior of quarks. Quantum chromodynamics (QCD) is a different world. […] Of course, that should not surprise us, because we’re talking very different order of magnitudes here: femtometers (10–15 m), in the case of electrons, as opposed to attometers (10–18 m) or even zeptometers (10–21 m) when we’re talking quarks.”
In fact, the femtometer scale is used to measure the radius of both protons as well as electrons and, hence, is much smaller than the atomic scale, which is measured in nanometer (1 nm = 10−9 m). The so-called Bohr radius for example, which is a measure for the size of an atom, is measured in nanometer indeed, so that’s a scale that is a million times larger than the femtometer scale. This gap in the scale effectively separates entirely different worlds. In fact, the gap is probably as large a gap as the gap between our macroscopic world and the strange reality of quantum mechanics. What happens at the femtometer scale, really?
The honest answer is: we don’t know, but we do have models to describe what happens. Moreover, for want of better models, physicists sort of believe these models are credible. To be precise, we assume there’s a force down there which we refer to as the strong force. In addition, there’s also a weak force. Now, you probably know these forces are modeled as interactions involving an exchange of virtual particles. This may be related to what Aitchison and Hey refer to as the physicist’s “distaste for action-at-a-distance.” To put it simply: if one particle – through some force – influences some other particle, then something must be going on between the two of them.
Of course, now you’ll say that something is effectively going on: there’s the electromagnetic field, right? Yes. But what’s the field? You’ll say: waves. But then you know electromagnetic waves also have a particle aspect. So we’re stuck with this weird theoretical framework: the conceptual distinction between particles and forces, or between particle and field, are not so clear. So that’s what the more advanced theories we’ll be looking at – like quantum field theory – try to bring together.
Note that we’ve been using a lot of confusing and/or ambiguous terms here: according to at least one leading physicist, for example, virtual particles should not be thought of as particles! But we’re putting the cart before the horse here. Let’s go step by step. To better understand the ‘mechanics’ of how the strong and weak interactions are being modeled in physics, most textbooks – including Aitchison and Hey, which we’ll follow here – start by explaining the original ideas as developed by the Japanese physicist Hideki Yukawa, who received a Nobel Prize for his work in 1949.
So what is it all about? As said, the ideas – or the model as such, so to speak – are more important than Yukawa’s original application, which was to model the force between a proton and a neutron. Indeed, we now explain such force as a force between quarks, and the force carrier is the gluon, which carries the so-called color charge. To be precise, the force between protons and neutrons – i.e. the so-called nuclear force – is now considered to be a rather minor residual force: it’s just what’s left of the actual strong force that binds quarks together. The Wikipedia article on this has some good text and a really nice animation on this. But… Well… Again, note that we are only interested in the model right now. So how does that look like?
First, we’ve got the equivalent of the electric charge: the nucleon is supposed to have some ‘strong’ charge, which we’ll write as gs. Now you know the formulas for the potential energy – because of the gravitational force – between two masses, or the potential energy between two charges – because of the electrostatic force. Let me jot them down once again:
- U(r) = –G·M·m/r
- U(r) = (1/4πε0)·q1·q2/r
The two formulas are exactly the same. They both assume U = 0 for r → ∞. Therefore, U(r) is always negative. [Just think of q1 and q2 as opposite charges, so the minus sign is not explicit – but it is also there!] We know that U(r) curve will look like the one below: some work (force times distance) is needed to move the two charges some distance away from each other – from point 1 to point 2, for example. [The distance r is x here – but you got that, right?]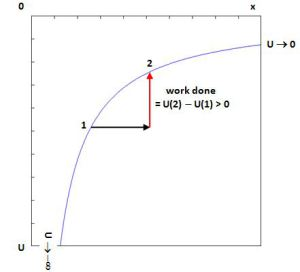
Now, physics textbooks – or other articles you might find, like on Wikipedia – will sometimes mention that the strong force is non-linear, but that’s very confusing because… Well… The electromagnetic force – or the gravitational force – aren’t linear either: their strength is inversely proportional to the square of the distance and – as you can see from the formulas for the potential energy – that 1/r factor isn’t linear either. So that isn’t very helpful. In order to further the discussion, I should now write down Yukawa’s hypothetical formula for the potential energy between a neutron and a proton, which we’ll refer to, logically, as the n-p potential: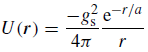 The −gs2 factor is, obviously, the equivalent of the q1·q2 product: think of the proton and the neutron having equal but opposite ‘strong’ charges. The 1/4π factor reminds us of the Coulomb constant: ke = 1/4πε0. Note this constant ensures the physical dimensions of both sides of the equation make sense: the dimension of ε0 is N·m2/C2, so U(r) is – as we’d expect – expressed in newton·meter, or joule. We’ll leave the question of the units for gs open – for the time being, that is. [As for the 1/4π factor, I am not sure why Yukawa put it there. My best guess is that he wanted to remind us some constant should be there to ensure the units come out alright.]
The −gs2 factor is, obviously, the equivalent of the q1·q2 product: think of the proton and the neutron having equal but opposite ‘strong’ charges. The 1/4π factor reminds us of the Coulomb constant: ke = 1/4πε0. Note this constant ensures the physical dimensions of both sides of the equation make sense: the dimension of ε0 is N·m2/C2, so U(r) is – as we’d expect – expressed in newton·meter, or joule. We’ll leave the question of the units for gs open – for the time being, that is. [As for the 1/4π factor, I am not sure why Yukawa put it there. My best guess is that he wanted to remind us some constant should be there to ensure the units come out alright.]
So, when everything is said and done, the big new thing is the e−r/a/r factor, which replaces the usual 1/r dependency on distance. Needless to say, e is Euler’s number here – not the electric charge. The two green curves below show what the e−r/a factor does to the classical 1/r function for a = 1 and a = 0.1 respectively: smaller values for a ensure the curve approaches zero more rapidly. In fact, for a = 1, e−r/a/r is equal to 0.368 for r = 1, and remains significant for values r that are greater than 1 too. In contrast, for a = 0.1, e−r/a/r is equal to 0.004579 (more or less, that is) for r = 4 and rapidly goes to zero for all values greater than that.

 Aitchison and Hey call a, therefore, a range parameter: it effectively defines the range in which the n-p potential has a significant value: outside of the range, its value is, for all practical purposes, (close to) zero. Experimentally, this range was established as being more or less equal to r ≤ 2 fm. Needless to say, while this range factor may do its job, it’s obvious Yukawa’s formula for the n-p potential comes across as being somewhat random: what’s the theory behind? There’s none, really. It makes one think of the logistic function: the logistic function fits many statistical patterns, but it is (usually) not obvious why.
Aitchison and Hey call a, therefore, a range parameter: it effectively defines the range in which the n-p potential has a significant value: outside of the range, its value is, for all practical purposes, (close to) zero. Experimentally, this range was established as being more or less equal to r ≤ 2 fm. Needless to say, while this range factor may do its job, it’s obvious Yukawa’s formula for the n-p potential comes across as being somewhat random: what’s the theory behind? There’s none, really. It makes one think of the logistic function: the logistic function fits many statistical patterns, but it is (usually) not obvious why.
Next in Yukawa’s argument is the establishment of an equivalent, for the nuclear force, of the Poisson equation in electrostatics: using the E = –∇Φ formula, we can re-write Maxwell’s ∇•E = ρ/ε0 equation (aka Gauss’ Law) as ∇•E = –∇•∇Φ = –∇2Φ ⇔ ∇2Φ= –ρ/ε0 indeed. The divergence operator the ∇• operator gives us the volume density of the flux of E out of an infinitesimal volume around a given point. [You may want to check one of my post on this. The formula becomes somewhat more obvious if we re-write it as ∇•E·dV = –(ρ·dV)/ε0: ∇•E·dV is then, quite simply, the flux of E out of the infinitesimally small volume dV, and the right-hand side of the equation says this is given by the product of the charge inside (ρ·dV) and 1/ε0, which accounts for the permittivity of the medium (which is the vacuum in this case).] Of course, you will also remember the ∇Φ notation: ∇ is just the gradient (or vector derivative) of the (scalar) potential Φ, i.e. the electric (or electrostatic) potential in a space around that infinitesimally small volume with charge density ρ. So… Well… The Poisson equation is probably not so obvious as it seems at first (again, check my post on it on it for more detail) and, yes, that ∇• operator – the divergence operator – is a pretty impressive mathematical beast. However, I must assume you master this topic and move on. So… Well… I must now give you the equivalent of Poisson’s equation for the nuclear force. It’s written like this: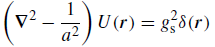 What the heck? Relax. To derive this equation, we’d need to take a pretty complicated détour, which we won’t do. [See Appendix G of Aitchison and Grey if you’d want the details.] Let me just point out the basics:
What the heck? Relax. To derive this equation, we’d need to take a pretty complicated détour, which we won’t do. [See Appendix G of Aitchison and Grey if you’d want the details.] Let me just point out the basics:
1. The Laplace operator (∇2) is replaced by one that’s nearly the same: ∇2 − 1/a2. And it operates on the same concept: a potential, which is a (scalar) function of the position r. Hence, U(r) is just the equivalent of Φ.
2. The right-hand side of the equation involves Dirac’s delta function. Now that’s a weird mathematical beast. Its definition seems to defy what I refer to as the ‘continuum assumption’ in math. I wrote a few things about it in one of my posts on Schrödinger’s equation – and I could give you its formula – but that won’t help you very much. It’s just a weird thing. As Aitchison and Grey write, you should just think of the whole expression as a finite range analogue of Poisson’s equation in electrostatics. So it’s only for extremely small r that the whole equation makes sense. Outside of the range defined by our range parameter a, the whole equation just reduces to 0 = 0 – for all practical purposes, at least.
Now, of course, you know that the neutron and the proton are not supposed to just sit there. They’re also in these sort of intricate dance which – for the electron case – is described by some wavefunction, which we derive as a solution from Schrödinger’s equation. So U(r) is going to vary not only in space but also in time and we should, therefore, write it as U(r, t). Now, we will, of course, assume it’s going to vary in space and time as some wave and we may, therefore, suggest some wave equation for it. To appreciate this point, you should review some of the posts I did on waves. More in particular, you may want to review the post I did on traveling fields, in which I showed you the following: if we see an equation like: then the function ψ(x, t) must have the following general functional form:
then the function ψ(x, t) must have the following general functional form: Any function ψ like that will work – so it will be a solution to the differential equation – and we’ll refer to it as a wavefunction. Now, the equation (and the function) is for a wave traveling in one dimension only (x) but the same post shows we can easily generalize to waves traveling in three dimensions. In addition, we may generalize the analyse to include complex-valued functions as well. Now, you will still be shocked by Yukawa’s field equation for U(r, t) but, hopefully, somewhat less so after the above reminder on how wave equations generally look like:
Any function ψ like that will work – so it will be a solution to the differential equation – and we’ll refer to it as a wavefunction. Now, the equation (and the function) is for a wave traveling in one dimension only (x) but the same post shows we can easily generalize to waves traveling in three dimensions. In addition, we may generalize the analyse to include complex-valued functions as well. Now, you will still be shocked by Yukawa’s field equation for U(r, t) but, hopefully, somewhat less so after the above reminder on how wave equations generally look like: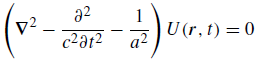 As said, you can look up the nitty-gritty in Aitchison and Grey (or in its appendices) but, up to this point, you should be able to sort of appreciate what’s going on without getting lost in it all. Yukawa’s next step – and all that follows – is much more baffling. We’d think U, the nuclear potential, is just some scalar-valued wave, right? It varies in space and in time, but… Well… That’s what classical waves, like water or sound waves, for example do too. So far, so good. However, Yukawa’s next step is to associate a de Broglie-type wavefunction with it. Hence, Yukawa imposes solutions of the type:
As said, you can look up the nitty-gritty in Aitchison and Grey (or in its appendices) but, up to this point, you should be able to sort of appreciate what’s going on without getting lost in it all. Yukawa’s next step – and all that follows – is much more baffling. We’d think U, the nuclear potential, is just some scalar-valued wave, right? It varies in space and in time, but… Well… That’s what classical waves, like water or sound waves, for example do too. So far, so good. However, Yukawa’s next step is to associate a de Broglie-type wavefunction with it. Hence, Yukawa imposes solutions of the type: What? Yes. It’s a big thing to swallow, and it doesn’t help most physicists refer to U as a force field. A force and the potential that results from it are two different things. To put it simply: the force on an object is not the same as the work you need to move it from here to there. Force and potential are related but different concepts. Having said that, it sort of make sense now, doesn’t it? If potential is energy, and if it behaves like some wave, then we must be able to associate it with a de Broglie-type particle. This U-quantum, as it is referred to, comes in two varieties, which are associated with the ongoing absorption-emission process that is supposed to take place inside of the nucleus (depicted below):
What? Yes. It’s a big thing to swallow, and it doesn’t help most physicists refer to U as a force field. A force and the potential that results from it are two different things. To put it simply: the force on an object is not the same as the work you need to move it from here to there. Force and potential are related but different concepts. Having said that, it sort of make sense now, doesn’t it? If potential is energy, and if it behaves like some wave, then we must be able to associate it with a de Broglie-type particle. This U-quantum, as it is referred to, comes in two varieties, which are associated with the ongoing absorption-emission process that is supposed to take place inside of the nucleus (depicted below):
p + U− → n and n + U+ → p

It’s easy to see that the U− and U+ particles are just each other’s anti-particle. When thinking about this, I can’t help remembering Feynman, when he enigmatically wrote – somewhere in his Strange Theory of Light and Matter – that an anti-particle might just be the same particle traveling back in time. In fact, the exchange here is supposed to happen within a time window that is so short it allows for the brief violation of the energy conservation principle.
Let’s be more precise and try to find the properties of that mysterious U-quantum. You’ll need to refresh what you know about operators to understand how substituting Yukawa’s de Broglie wavefunction in the complicated-looking differential equation (the wave equation) gives us the following relation between the energy and the momentum of our new particle: Now, it doesn’t take too many gimmicks to compare this against the relativistically correct energy-momentum relation:
Now, it doesn’t take too many gimmicks to compare this against the relativistically correct energy-momentum relation: Combining both gives us the associated (rest) mass of the U-quantum:
Combining both gives us the associated (rest) mass of the U-quantum: For a ≈ 2 fm, mU is about 100 MeV. Of course, it’s always to check the dimensions and calculate stuff yourself. Note the physical dimension of ħ/(a·c) is N·s2/m = kg (just think of the F = m·a formula). Also note that N·s2/m = kg = (N·m)·s2/m2 = J/(m2/s2), so that’s the [E]/[c2] dimension. The calculation – and interpretation – is somewhat tricky though: if you do it, you’ll find that:
For a ≈ 2 fm, mU is about 100 MeV. Of course, it’s always to check the dimensions and calculate stuff yourself. Note the physical dimension of ħ/(a·c) is N·s2/m = kg (just think of the F = m·a formula). Also note that N·s2/m = kg = (N·m)·s2/m2 = J/(m2/s2), so that’s the [E]/[c2] dimension. The calculation – and interpretation – is somewhat tricky though: if you do it, you’ll find that:
ħ/(a·c) ≈ (1.0545718×10−34 N·m·s)/[(2×10−15 m)·(2.997924583×108 m/s)] ≈ 0.176×10−27 kg
Now, most physics handbooks continue that terrible habit of writing particle weights in eV, rather than using the correct eV/c2 unit. So when they write: mU is about 100 MeV, they actually mean to say that it’s 100 MeV/c2. In addition, the eV is not an SI unit. Hence, to get that number, we should first write 0.176×10−27 kg as some value expressed in J/c2, and then convert the joule (J) into electronvolt (eV). Let’s do that. First, note that c2 ≈ 9×1016 m2/s2, so 0.176×10−27 kg ≈ 1.584×10−11 J/c2. Now we do the conversion from joule to electronvolt. We get: (1.584×10−11 J/c2)·(6.24215×1018 eV/J) ≈ 9.9×107 eV/c2 = 99 MeV/c2. Bingo! So that was Yukawa’s prediction for the nuclear force quantum.
Of course, Yukawa was wrong but, as mentioned above, his ideas are now generally accepted. First note the mass of the U-quantum is quite considerable: 100 MeV/c2 is a bit more than 10% of the individual proton or neutron mass (about 938-939 MeV/c2). While the binding energy causes the mass of an atom to be less than the mass of their constituent parts (protons, neutrons and electrons), it’s quite remarkably that the deuterium atom – a hydrogen atom with an extra neutron – has an excess mass of about 13.1 MeV/c2, and a binding energy with an equivalent mass of only 2.2 MeV/c2. So… Well… There’s something there.
As said, this post only wanted to introduce some basic ideas. The current model of nuclear physics is represented by the animation below, which I took from the Wikipedia article on it. The U-quantum appears as the pion here – and it does not really turn the proton into a neutron and vice versa. Those particles are assumed to be stable. In contrast, it is the quarks that change color by exchanging gluons between each other. And we know look at the exchange particle – which we refer to as the pion – between the proton and the neutron as consisting of two quarks in its own right: a quark and a anti-quark. So… Yes… All weird. QCD is just a different world. We’ll explore it more in the coming days and/or weeks. 🙂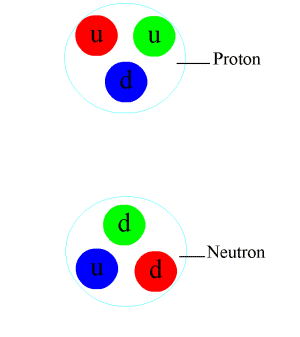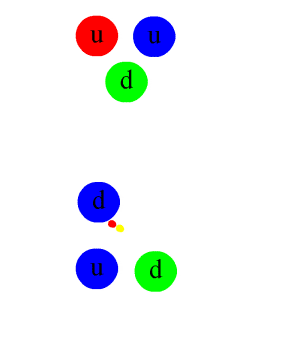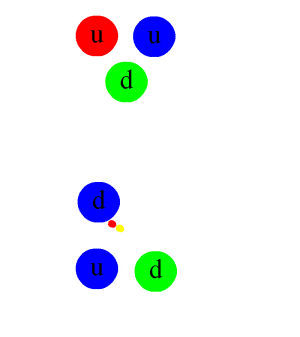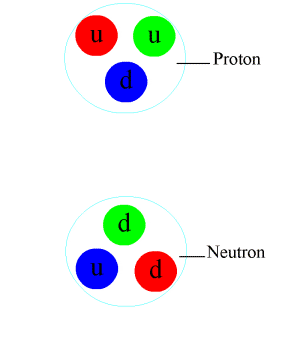 An alternative – and simpler – way of representing this exchange of a virtual particle (a neutral pion in this case) is obtained by drawing a so-called Feynman diagram:
An alternative – and simpler – way of representing this exchange of a virtual particle (a neutral pion in this case) is obtained by drawing a so-called Feynman diagram: OK. That’s it for today. More tomorrow. 🙂
OK. That’s it for today. More tomorrow. 🙂
Some content on this page was disabled on June 20, 2020 as a result of a DMCA takedown notice from Michael A. Gottlieb, Rudolf Pfeiffer, and The California Institute of Technology. You can learn more about the DMCA here:
https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on June 20, 2020 as a result of a DMCA takedown notice from Michael A. Gottlieb, Rudolf Pfeiffer, and The California Institute of Technology. You can learn more about the DMCA here:
https://wordpress.com/support/copyright-and-the-dmca/


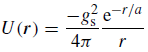 The −g
The −g
 Aitchison and Hey call a, therefore, a range parameter: it effectively defines the range in which the n-p potential has a significant value: outside of the range, its value is, for all practical purposes, (close to) zero. Experimentally, this range was established as being more or less equal to r ≤ 2 fm. Needless to say, while this range factor may do its job, it’s obvious Yukawa’s formula for the n-p potential comes across as being somewhat random: what’s the theory behind? There’s none, really. It makes one think of
Aitchison and Hey call a, therefore, a range parameter: it effectively defines the range in which the n-p potential has a significant value: outside of the range, its value is, for all practical purposes, (close to) zero. Experimentally, this range was established as being more or less equal to r ≤ 2 fm. Needless to say, while this range factor may do its job, it’s obvious Yukawa’s formula for the n-p potential comes across as being somewhat random: what’s the theory behind? There’s none, really. It makes one think of 
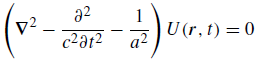 As said, you can look up the nitty-gritty in
As said, you can look up the nitty-gritty in 
 Now, it doesn’t take too many gimmicks to compare this against the relativistically correct energy-momentum relation:
Now, it doesn’t take too many gimmicks to compare this against the relativistically correct energy-momentum relation: An alternative – and simpler – way of representing this exchange of a virtual particle (a neutral pion in this case) is obtained by drawing a so-called Feynman diagram:
An alternative – and simpler – way of representing this exchange of a virtual particle (a neutral pion in this case) is obtained by drawing a so-called Feynman diagram: OK. That’s it for today. More tomorrow. 🙂
OK. That’s it for today. More tomorrow. 🙂