Pre-scriptum (dated 26 June 2020): These posts on elementary math and physics have not suffered much (if at all) from the attack by the dark force—which is good because I still like them. While my views on the true nature of light, matter and the force or forces that act on them have evolved significantly as part of my explorations of a more realist (classical) explanation of quantum mechanics, I think most (if not all) of the analysis in this post remains valid and fun to read. In fact, I find the simplest stuff is often the best. 🙂
Original post:
When introducing mirror symmetry (P-symmetry) in one of my older posts (time reversal and CPT-symmetry), I also introduced the concept of axial and polar vectors in physics. Axial vectors have to do with rotations, or spinning objects. Because spin – i.e. turning motion – is such an important concept in physics, I’d suggest we re-visit the topic here.
Of course, I should be clear from the outset that the discussion below is entirely classical. Indeed, as Wikipedia puts it: “The intrinsic spin of elementary particles (such as electrons) is quantum-mechanical phenomenon that does not have a counterpart in classical mechanics, despite the term spin being reminiscent of classical phenomena such as a planet spinning on its axis.” Nevertheless, if we don’t understand what spin is in the classical world – i.e. our world for all practical purposes – then we won’t get even near to appreciating what it might be in the quantum-mechanical world. Besides, it’s just plain fun: I am sure you have played, as a kid of as an adult even, with one of those magical spinning tops or toy gyroscopes and so you probably wonder how it really works in physics. So that’s what this post is all about.
The essential concept is the concept of torque. For rotations in space (i.e. rotational motion), the torque is what the force is for linear motion:
- It’s the torque (τ) that makes an object spin faster or slower, just like the force would accelerate or decelerate that very same object when it would be moving along some curve (as opposed to spinning around some axis).
- There’s also a similar ‘law of Newton’ for torque: you’ll remember that the force equals the time rate-of-change of a vector quantity referred to as (linear) momentum: F = dp/dt = d(mv)/dt = ma (the mass times the acceleration). Likewise, we have a vector quantity that is referred to as angular momentum (L), and we can write: τ (i.e. the Greek tau) = dL/dt.
- Finally, instead of linear velocity, we’ll have an angular velocity ω (omega), which is the time rate-of-change of the angle θ defining how far the object has gone around (as opposed to the distance in linear dynamics, describing how far the object has gone along). So we have ω = dθ/dt. This is actually easy to visualize because we know that θ is the length of the corresponding arc on the unit circle. Hence, the equivalence with the linear distance traveled is easily ascertained.
There are numerous other equivalences. For example, we also have an angular acceleration: α = dω/dt = d2θ/dt2; and we should also note that, just like the force, the torque is doing work – in its conventional definition as used in physics – as it turns an object:
ΔW = τ·Δθ
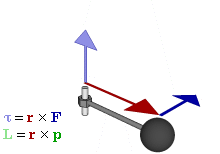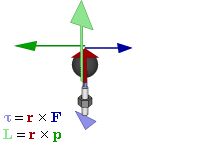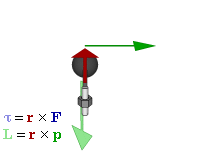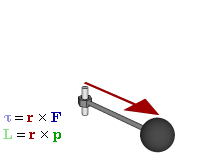
However, we also need to point out the differences. The animation below does that very well, as it relates the ‘new’ concepts – i.e. torque and angular momentum – to the ‘old’ concepts – i.e. force and linear momentum.
So what do we have here? We have vector quantities once again, denoted by symbols in bold-face. However, τ, L and ω are special vectors: axial vectors indeed, as opposed to the polar vectors F, p and v. Axial vectors are directed along the axis of spin – so that is, strangely enough, at right angles to the direction of spin, or perpendicular to the ‘plane of the twist’ as Feynman calls it – and the direction of the axial vector is determined by the direction of spin through one of two conventions: the ‘right-hand screw rule’ or the ‘left-hand screw rule’. Physicists have settled on the former.
If you feel very confused now (I did when I first looked at it), just step back and go through the full argument as I develop it here. It helps to think of torque (also known, for some obscure reason, as the moment of the force) as a twist on an object or a plane indeed: the torque’s magnitude is equal to the tangential component of the force, i.e. F·sin(Δθ), times the distance between the object and the axis of rotation (we’ll denote this distance by r). This quantity is also equal to the product of the magnitude of the force itself and the length of the so-called lever arm, i.e. the perpendicular distance from the axis to the line of action of the force (this lever arm length is denoted by r0). So we can write τ as:
- The product of the tangential component of the force times the distance r: τ = r·Ft = r·F·sin(Δθ)
- The product of the length of the lever arm times the force: τ = r0·F
- The torque is the work done per unit of distance traveled: τ = ΔW/Δθ or τ = dW/dθ in the limit.
So… These are actually only the basics, which you should remember from your high-school physics course. If not, have another look at it. We now need to go from scalar quantities to vector quantities to understand that animation above. Torque is not a vector like force or velocity, not a priori at least. However, we can associate torque with a vector of a special type, an axial vector. Feynman calls vectors such as force or (linear) velocity ‘honest’ or ‘real’ vectors. The mathematically correct term for such ‘honest’ or ‘real’ vectors is polar vector. Hence, axial vectors are not ‘honest’ or ‘real’ in some sense: we derive them from the polar vectors. They are, in effect, a so-called cross product of two ‘honest’ vectors. Here we need to explain the difference between a dot and a cross product between two vectors once again:
(1) A dot product, which we denoted by a little dot (·), yields a scalar quantity: a·b = |a||b|cosα = a·b·cosα with α the angle between the two vectors a and b. Note that the dot product of two orthogonal vectors is equal to zero, so take care: τ = r·Ft = r·F·sin(Δθ) is not a dot product of two vectors. It’s a simple product of two scalar quantities: we only use the dot as a mark of separation, which may be quite confusing. In fact, some authors use ∗ for a product of scalars to avoid confusion: that’s not a bad idea, but it’s not a convention as yet. Omitting the dot when multiplying scalars (as I do when I write |a||b|cosα) is also possible, but it makes it a bit difficult to read formulas I find. Also note, once again, how important the difference between bold-face and normal type is in formulas like this: it distinguishes vectors from scalars – and these are two very different things indeed.
(2) A cross product, which we denote by using a cross (×), yields another vector: τ = r×F =|r|·|F|·sinα·n = r·F·sinα·n with n the normal unit vector given by the right-hand rule. Note how a cross product involves a sine, not a cosine – as opposed to a dot product. Hence, if r and F are orthogonal vectors (which is not unlikely), then this sine term will be equal to 1. If the two vectors are not perpendicular to each other, then the sine function will assure that we use the tangential component of the force.
But, again, how do we go from torque as a scalar quantity (τ = r·Ft) to the vector τ = r×F? Well… Let’s suppose, first, that, in our (inertial) frame of reference, we have some object spinning around the z-axis only. In other words, it spins in the xy-plane only. So we have a torque around (or about) the z-axis, i.e. in the xy-plane. The work that will be done by this torque can be written as:
ΔW = FxΔx + FyΔy = (xFy – yFx)Δθ
Huh? Yes. This results from a simple two-dimensional analysis of what’s going on in the xy-plane: the force has an x- and a y-component, and the distance traveled in the x- and y-direction is Δx = –yΔθ and Δy = xΔθ respectively. I won’t go into the details of this (you can easily find these elsewhere) but just note the minus sign for Δx and the way the x and y get switched in the expressions.
So the torque in the xy-plane is given by τxy = ΔW/Δθ = xFy – yFx. Likewise, if the object would be spinning about the x-axis – or, what amounts to the same, in the yz-plane – we’d get τyz = yFz – zFy. Finally, for some object spinning about the y-axis (i.e. in the zx-plane – and please note I write zx, not xz, so as to be consistent as we switch the order of the x, y and z coordinates in the formulas), then we’d get τzx = zFx – xFz. Now we can appreciate the fact that a torque in some other plane, at some angle with our Cartesian planes, would be some combination of these three torques, so we’d write:
(1) τxy = xFy – yFx
(2) τyz = yFz – zFy and
(3) τzx = zFx – xFz.
Another observer with his Cartesian x’, y’ and z’ axes in some other direction (we’re not talking some observer moving away from us but, quite simply, a reference frame that’s being rotated itself around some axis not necessarily coinciding with any of the x-, y- z- or x’-, y’- and z’-axes mentioned above) would find other values as he calculates these torques, but the formulas would look the same:
(1’) τx’y’ = x’Fy’ – y’Fx’
(2’) τy’z’ = y’Fz’ – z’Fy’ and
(3’) τz’x’ = z’Fx’ – x’Fz’.
Now, of course, there must be some ‘nice’ relationship that expresses the τx’y’, τy’z’ and τz’x’ values in terms of τxy, τyz, just like there was some ‘nice’ relationship between the x’, y’ and z’ components of a vector in one coordination system (the x’, y’ and z’ coordinate system) and the x, y, z components of that same vector in the x, y and z coordinate system. Now, I won’t go into the details but that ‘nice’ relationship is, in fact, given by transformation expressions involving a rotation matrix. I won’t write that one down here, because it looks pretty formidable, but just google ‘axis-angle representation of a rotation’ and you’ll get all the details you want.
The point to note is that, in both sets of equations above, we have an x-, y- and z-component of some mathematical vector that transform just like a ‘real’ vector. Now, if it behaves like a vector, we’ll just call it a vector, and that’s how, in essence, we define torque, angular momentum (and angular velocity too) as axial vectors. We should note how it works exactly though:
(1) τxy and τx’y’ will transform like the z-component of a vector (note that we were talking rotational motion about the z-axis when introducing this quantity);
(2) τyz and τy’z’ will transform like the x-component of a vector (note that we were talking rotational motion about the x-axis when introducing this quantity);
(3) τzx and τz’x’ will transform like the y-component of a vector (note that we were talking rotation motion when introducing this quantity). So we have
τ = (τyz, τzx, τxy) = (τx, τy, τz) with
τx = τyz = yFz – zFy
τy = τzx = zFx – xFz
τz = τxy = xFy – yFx.
[This may look very difficult to remember but just look at the order: all we do is respect the clockwise order x, y, z, x, y, z, x, etc. when jotting down the x, y and z subscripts.]
Now we are, finally, well equipped to once again look at that vector representation of rotation. I reproduce it once again below so you don’t have to scroll back to that animation:
We have rotation in the zx-plane here (i.e. rotation about the y-axis) driven by an oscillating force F, and so, yes, we can see that the torque vector oscillates along the y-axis only: its x- and z-components are zero. We also have L here, the angular momentum. That’s a vector quantity as well. We can write it as
L = (Lyz, Lzx, Lxy) = (Lx, Ly, Lz) with
Lx = Lyz = ypz – zpy (i.e. the angular momentum about the x-axis)
Ly = Lzx = zpx – xpz (i.e. the angular momentum about the y-axis)
Lz = Lxy = xpy – ypx (i.e. the angular momentum about the z-axis),
And we note, once again, that only the y-component is non-zero in this case, because the rotation is about the y-axis.
We should now remember the rules for a cross product. Above, we wrote that τ = r´F =|r|×|F|×sina×n = = r×F×sina×n with n the normal unit vector given by the right-hand rule. However, a vector product can also be written in terms of its components: c = a´b if and only
cx = aybz – azby,
cy = azbx – axbz, and
cz = axby – aybx.
Again, if this looks difficult, remember the trick above: respect the clockwise order when jotting down the x, y and z subscripts. I’ll leave it to you to work out r´F and r´p in terms of components but, when you write it all out, you’ll see it corresponds to the formulas above. In addition, I will also leave it to you to show that the velocity of some particle in a rotating body can be given by a similar vector product: v = ω´r, with ω being defined as another axial vector (aka pseudovector) pointing along the direction of the axis of rotation, i.e. not in the direction of motion. [Is that strange? No. As it’s rotational motion, there is no ‘direction of motion’ really: the object, or any particle in that object, goes round and round and round indeed and, hence, defining some normal vector using the right-hand rule to denote angular velocity makes a lot of sense.]
I could continue to write and write and write, but I need to stop here. Indeed, I actually wanted to tell you how gyroscopes work, but I notice that this introduction has already taken several pages. Hence, I’ll leave the gyroscope for a separate post. So, be warned, you’ll need to read and understand this one before reading my next one.

Great site you’ve got here.. It’s hard to find high-quality writing
like yours these days. I really appreciate people like you!
Take care!!