Pre-script (dated 26 June 2020): Our ideas have evolved into a full-blown realistic (or classical) interpretation of all things quantum-mechanical. In addition, I note the dark force has amused himself by removing some material. So no use to read this. Read my recent papers instead. 🙂
Original post:
My previous post explained how four-vectors transform from one reference frame to the other. Indeed, a four-vector is not just some one-dimensional array of four numbers: it represent something—a physical vector that… Well… Transforms like a vector. 🙂 So what vectors are we talking about? Let’s see what we have:
- We knew the position four-vector already, which we’ll write as xμ = (ct, x, y, z) = (ct, x).
- We also proved that Aμ = (Φ, Ax, Ay, Az) = (Φ, A) is a four-vector: it’s referred to as the four-potential.
- We also know the momentum four-vector from the Lectures on special relativity. We write it as pμ = (E, px, py, pz) = (E, p), with E = γm0, p = γm0v, and γ = (1−v2/c2)−1/2 or, for c = 1, γ = (1−v2)−1/2
To show that it’s not just a matter of adding some fourth t-component to a three-vector, Feynman gives the example of the four-velocity vector. We have vx = dx/dt, vy = dy/dt and vz = dz/dt, but a vμ = (d(ct)/dt, dx/dt, dy/dt, dz/dt) = (c, dx/dt, dy/dt, dz/dt) ‘vector’ is, obviously, not a four-vector. [Why obviously? The inner product vμvμ is not invariant.] In fact, Feynman ‘fixes’ the problem by noting that ct, x, y and z have the ‘right behavior’, but the d/dt operator doesn’t. The d/dt operator is not an invariant operator. So how does he fix it then? He tries the (1−v2/c2)−1/2·d/dt operator and, yes, it turns out we do get a four-vector then. In fact, we get that four-velocity vector uμ that we were looking for:
[Note we assume we’re using equivalent time and distance units now, so c = 1 and v/c reduces to a new variable v.]
Now how do we know this is four-vector? How can we prove this one? It’s simple. We can get it from our pμ = (E, p) by dividing it by m0, which is an invariant scalar in four dimensions too. Now, it is easy to see that a division by an invariant scalar does not change the transformation properties. So just write it all out, and you’ll see that pμ/m0 = uμ and, hence, that uμ is a four-vector too. 🙂
We’ve got an interesting thing here actually: division by an invariant scalar, or applying that (1−v2/c2)−1/2·d/dt operator, which is referred to as an invariant operator, on a four-vector will give us another four-vector. Why is that? Let’s switch to compatible time and distance units so c = 1 so to simplify the analysis that follows.
The invariant (1−v2)−1/2·d/dt operator and the proper time s
Why is the (1−v2)−1/2·d/dt operator invariant? Why does it ‘fix’ things? Well… Think about the invariant spacetime interval (Δs)2 = Δt2 − Δx2 − Δy2 − Δz2 going to the limit (ds)2 = dt2 − dx2 − dy2 − dz2 . Of course, we can and should relate this to an invariant quantity s = ∫ ds. Just like Δs, this quantity also ‘mixes’ time and distance. Now, we could try to associate some derivative d/ds with it because, as Feynman puts it, “it should be a nice four-dimensional operation because it is invariant with respect to a Lorentz transformation.” Yes. It should be. So let’s relate ds to dt and see what we get. That’s easy enough: dx = vx·dt, dy = vy·dt, dz = vz·dt, so we write:
(ds)2 = dt2 − vx2·dt2 − vy2·dt2 − vz2·dt2 ⇔ (ds)2 = dt2·(1 − vx2 − vy2 − vz2) = dt2·(1 − v2)
and, therefore, ds = dt·(1−v2)1/2. So our operator d/ds is equal to (1−v2)−1/2·d/dt, and we can apply it to any four-vector, as we are sure that, as an invariant operator, it’s going to give us another four-vector. I’ll highlight the result, because it’s important:
The d/ds = (1−v2)−1/2·d/dt operator is an invariant operator for four-vectors.
For example, if we apply it to xμ = (t, x, y, z), we get the very same four-velocity vector μμ:
dxμ/ds = uμ = pμ/m0
Now, if you’re somewhat awake, you should ask yourself: what is this s, really, and what is this operator all about? Our new function s = ∫ ds is not the distance function, as it’s got both time and distance in it. Likewise, the invariant operator d/ds = (1−v2)−1/2·d/dt has both time and distance in it (the distance is implicit in the v2 factor). Still, it is referred to as the proper time along the path of a particle. Now why is that? If it’s got distance and time in it, why don’t we call it the ‘proper distance-time’ or something?
Well… The invariant quantity s actually is the time that would be measured by a clock that’s moving along, in spacetime, with the particle. Just think of it: in the reference frame of the moving particle itself, Δx, Δy and Δz must be zero, because it’s not moving in its own reference frame. So the (Δs)2 = Δt2 − Δx2 − Δy2 − Δz2 reduces to (Δs)2 = Δt2, and so we’re only adding time to s. Of course, this view of things implies that the proper time itself is fixed only up to some arbitrary additive constant, namely the setting of the clock at some event along the ‘world line’ of our particle, which is its path in four-dimensional spacetime. But… Well… In a way, s is the ‘genuine’ or ‘proper’ time coming with the particle’s reference frame, and so that’s why Einstein called it like that. You’ll see (later) that it plays a very important role in general relativity theory (which is a topic we haven’t discussed yet: we’ve only touched special relativity, so no gravity effects).
OK. I know this is simple and complicated at the same time: the math is (fairly) easy but, yes, it may be difficult to ‘understand’ this in some kind of intuitive way. But let’s move on.
The four-force vector fμ
We know the relativistically correct equation for the motion of some charge q. It’s just Newton’s Law F = dp/dt = d(mv)/dt. The only difference is that we are not assuming that m is some constant. Instead, we use the p = γm0v formula to get:
How can we get a four-vector for the force? It turns out that we get it when applying our new invariant operator to the momentum four-vector pμ = (E, p), so we write: fμ = dpμ/ds. But pμ = m0uμ = m0dxμ/ds, so we can re-write this as fμ = d(m0·dxμ/ds)/ds, which gives us a formula which is reminiscent of the Newtonian F = ma equation:
What is this thing? Well… It’s not so difficult to verify that the x, y and z-components are just our old-fashioned Fx, Fy and Fz, so these are the components of F. The t-component is (1−v2)−1/2·dE/dt. Now, dE/dt is the time rate of change of energy and, hence, it’s equal to the rate of doing work on our charge, which is equal to F•v. So we can write fμ as:
The force and the tensor
We will now derive that formula which we ended the previous post with. We start with calculating the spacelike components of fμ from the Lorentz formula F = q(E + v×B). [The terminology is nice, isn’t it? The spacelike components of the four-force vector! Now that sounds impressive, doesn’t it? But so… Well… It’s really just the old stuff we know already.] So we start with fx = Fx, and write it all out:
What a monster! But, hey! We can ‘simplify’ this by substituting stuff by (1) the t-, x-, y- and z-components of the four-velocity vector uμ and (2) the components of our tensor Fμν = [Fij] = [∇iAj − ∇jAi] with i, j = t, x, y, z. We’ll also pop in the diagonal Fxx = 0 element, just to make sure it’s all there. We get:
Looks better, doesn’t it? 🙂 Of course, it’s just the same, really. This is just an exercise in symbolism. Let me insert the electromagnetic tensor we defined in our previous post, just as a reminder of what that Fμν matrix actually is:
If you read my previous post, this matrix – or the concept of a tensor – has no secrets for you. Let me briefly summarize it, because it’s an important result as well. The tensor is (a generalization of) the cross-product in four-dimensional space. We take two vectors: aμ = (at, ax, ay, az) and bμ = (bt, bx, by, bz) and then we take cross-products of their components just like we did in three-dimensional space, so we write Tij = aibj − ajbi. Now, it’s easy to see that this combination implies that Tij = − Tji and that Tii = 0, which is why we only have six independent numbers out of the 16 possible combinations, and which is why we’ll get a so-called anti-symmetric matrix when we organize them in a matrix. In three dimensions, the very same definition of the cross-product Tij gives us 9 combinations, and only 3 independent numbers, which is why we represented our ‘tensor’ as a vector too! In four-dimensional space we can’t do that: six things cannot be represented by a four-vector, so we need to use this matrix, which is referred to as a tensor of the second rank in four dimensions. [When you start using words like that, you’ve come a long way, really. :-)]
[…] OK. Back to our four-force. It’s easy to get a similar one-liner for fy and fz too, of course, as well as for ft. But… Yes, ft… Is it the same thing really? Let me quickly copy Feynman’s calculation for ft:
It does: remember that v×B and v are orthogonal, and so their dot product is zero indeed. So, to make a long story short, the four equations – one for each component of the four-force vector fμ – can be summarized in the following elegant equation:
Writing this all requires a few conventions, however. For example, Fμν is a 4×4 matrix and so uν has to be written as a 1×4 vector. And the formula for the fx and ft component also make it clear that we also want to use the +−−− signature here, so the convention for the signs in the uνFμν product is the same as that for the scalar product aμbμ. So, in short, you really need to interpret what’s being written here.
A more important question, perhaps, is: what can we do with it? Well… Feynman’s evaluation of the usefulness of this formula is rather succinct: “Although it is nice to see that the equations can be written that way, this form is not particularly useful. It’s usually more convenient to solve for particle motions by using the F = q(E + v×B) = (1−v2)−1/2·d(m0v)/dt equations, and that’s what we will usually do.”
Having said that, this formula really makes good on the promise I started my previous post with: we wanted a formula, some mathematical construct, that effectively presents the electromagnetic force as one force, as one physical reality. So… Well… Here it is! 🙂
Well… That’s it for today. Tomorrow we’ll talk about energy and about a very mysterious concept—the electromagnetic mass. That should be fun! So I’ll c u tomorrow! 🙂
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:
https://en.support.wordpress.com/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://en.support.wordpress.com/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://en.support.wordpress.com/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://en.support.wordpress.com/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://en.support.wordpress.com/copyright-and-the-dmca/
Some content on this page was disabled on June 16, 2020 as a result of a DMCA takedown notice from The California Institute of Technology. You can learn more about the DMCA here:https://en.support.wordpress.com/copyright-and-the-dmca/
Some content on this page was disabled on June 20, 2020 as a result of a DMCA takedown notice from Michael A. Gottlieb, Rudolf Pfeiffer, and The California Institute of Technology. You can learn more about the DMCA here:
Reading Feynman 
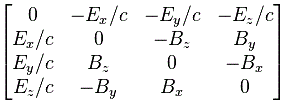
2 thoughts on “Re-visiting relativity and four-vectors: the proper time, the tensor and the four-force”