The Hamiltonian revisited

I want to come back to something I mentioned in a previous post: when looking at that formula for those U_ij amplitudes—which I’ll jot down once more:

U_ij(t + Δt, t) = δ_ij + ΔU_ij(t + Δt, t) = δ_ij + K_ij(t)·Δt ⇔ U_ij(t + Δt, t) = δ_ij − (i/ħ)·H_ij(t)·Δt

—I noted that it resembles the general y(t + Δt) = y(t) + Δy = y(t) + (dy/dt)·Δt formula. So we can look at our K_ij(t) function as being equal to the time derivative of the U_ij(t + Δt, t) function. I want to re-visit that here, as it triggers a whole range of questions, which may or may not help to understand quantum math somewhat more intuitively.  Let’s quickly sum up what we’ve learned so far: it’s basically all about quantum-mechanical stuff that does not move in space. Hence, the x in our wavefunction ψ(x, t) is some fixed point in space and, therefore, our elementary wavefunction—which we wrote as:

ψ(x, t) = a·e^−i·θ = a·e^{−i·(ω·t − k∙x)} = a·e^{−i·[(E/ħ)·t − (p/ħ)∙x]}

—reduces to ψ(t) = a·e^−i·ω·t = a·e^{−i·[(E/ħ)·t}.

Unlike what you might think, we’re not equating x with zero here. No. It’s the p = m·v factor that becomes zero, because our reference frame is that of the system that we’re looking at, so its velocity is zero: it doesn’t move in our reference frame. That immediately answers an obvious question: does our wavefunction look any different when choosing another reference frame? The answer is obviously: yes! It surely matters if the system moves or not, and it also matters how fast it moves, because it changes the energy and momentum values from E and p to some E’ and p’. However, we’ll not consider such complications here: that’s the realm of relativistic quantum mechanics. Let’s start with the simplest of situations.

A simple two-state system

One of the simplest examples of a quantum-mechanical system that does not move in space, is the textbook example of the ammonia molecule. The picture was as simple as the one below: an ammonia molecule consists of one nitrogen atom and three hydrogen atoms, and the nitrogen atom could be ‘up’ or ‘down’ with regard to the motion of the NH₃ molecule around its axis of symmetry, as shown below.

It’s important to note that this ‘up’ or ‘down’ direction is, once again, defined with respect to the reference frame of the system itself. The motion of the molecule around its axis of symmetry is referred to as its spin—a term that’s used in a variety of contexts and, therefore, is annoyingly ambiguous. When we use the term ‘spin’ (up or down) to describe an electron state, for example, we’d associate it with the direction of its magnetic moment. Such magnetic moment arises from the fact that, for all practical purposes, we can think of an electron as a spinning electric charge. Now, while our ammonia molecule is electrically neutral, as a whole, the two states are actually associated with opposite electric dipole moments, as illustrated below. Hence, when we’d apply an electric field (denoted as ε) below, the two states are effectively associated with different energy levels, which we wrote as E₀ ± εμ.

But we’re getting ahead of ourselves here. Let’s revert to the system in free space, i.e. without an electromagnetic force field—or, what amounts to saying the same, without potential. Now, the ammonia molecule is a quantum-mechanical system, and so there is some amplitude for the nitrogen atom to tunnel through the plane of hydrogens. I told you before that this is the key to understanding quantum mechanics really: there is an energy barrier there and, classically, the nitrogen atom should not sneak across. But it does. It’s like it can borrow some energy – which we denote by A – to penetrate the energy barrier.

In quantum mechanics, the dynamics of this system are modeled using a set of two differential equations. These differential equations are really the equivalent of Newton’s classical Law of Motion (I am referring to the F = m·(dv/dt) = m·a equation here) in quantum mechanics, so I’ll have to explain them—which is not so easy as explaining Newton’s Law, because we’re talking complex-valued functions, but… Well… Let me first insert the solution of that set of differential equations:

This graph shows how the probability of the nitrogen atom (or the ammonia molecule itself) being in state 1 (i.e. ‘up’) or, else, in state 2 (i.e. ‘down’), varies sinusoidally in time. Let me also give you the equations for the amplitudes to be in state 1 or 2 respectively:

1. C₁(t) = 〈 1 | ψ 〉 = (1/2)·e^{−(i/ħ)·(E₀ − A)·t} + (1/2)·e^{−(i/ħ)·(E₀ + A)·t} = e^{−(i/ħ)·E₀·t}·cos[(A/ħ)·t]
2. C₂(t) = 〈 2 | ψ 〉 = (1/2)·e^{−(i/ħ)·(E₀ − A)·t} – (1/2)·e^{−(i/ħ)·(E₀ + A)·t} = i·e^{−(i/ħ)·E₀·t}·sin[(A/ħ)·t]

So the P₁(t) and P₂(t) probabilities above are just the absolute square of these C₁(t) and C₂(t) functions. So as to help you understand what’s going on here, let me quickly insert the following technical remarks:

• In case you wonder how we go from those exponentials to a simple sine and cosine factor, remember that the sum of complex conjugates, i.e e^iθ + e^−iθ reduces to 2·cosθ, while e^iθ − e^−iθ reduces to 2·i·sinθ.
• As for how to take the absolute square… Well… I shouldn’t be explaining that here, but you should be able to work that out remembering that (i) |a·b·c|² = |a|²·|b|²·|c|²; (ii) |e^iθ|² = |e^−iθ|² = 1² = 1 (for any value of θ); and (iii) |i|² = 1.
• As for the periodicity of both probability functions, note that the period of the squared sine and cosine functions is equal to π. Hence, the argument of our sine and cosine function will be equal to 0, π, 2π, 3π etcetera if (A/ħ)·t = 0, π, 2π, 3π etcetera, i.e. if t = 0·ħ/A, π·ħ/A, 2π·ħ/A, 3π·ħ/A etcetera. So that’s why we measure time in units of ħ/A above.

The graph above is actually tricky to interpret, as it assumes that we know in what state the molecule starts out with at t = 0. This assumption is tricky because we usually do not know that: we have to make some observation which, curiously enough, will always yield one of the two states—nothing in-between. Or, else, we can use a state selector—an inhomogeneous electric field which will separate the ammonia molecules according to their state. It’s a weird thing really, and it summarizes all of the ‘craziness’ of quantum-mechanics: as long as we don’t measure anything – by applying that force field – our molecule is in some kind of abstract state, which mixes the two base states. But when we do make the measurement, always along some specific direction (which we usually take to be the z-direction in our reference frame), we’ll always find the molecule is either ‘up’ or, else, ‘down’. We never measure it as something in-between. Personally, I like to think the measurement apparatus – I am talking the electric field here – causes the nitrogen atom to sort of ‘snap into place’. However, physicists use more precise language here: they would say that the electric field does result in the two positions having very different energy levels (E₀ + εμ and E₀ – εμ, to be precise) and that, as a result, the amplitude for the nitrogen atom to flip back and forth has little effect. Now how do we model that?

The Hamiltonian equations

I shouldn’t be using the term above, as it usually refers to a set of differential equations describing classical systems. However, I’ll also use it for the quantum-mechanical analog, which amounts to the following for our simple two-state example above:

Don’t panic. We’ll explain. The equations above are all the same but use different formats: the first block writes them as a set of equations, while the second uses the matrix notation, which involves the use of that rather infamous Hamiltonian matrix, which we denote by H = [H_ij]. Now, we’ve postponed a lot of technical stuff, so… Well… We can’t avoid it any longer. Let’s look at those Hamiltonian coefficients H_ij first. Where do they come from?

You’ll remember we thought of time as some kind of apparatus, with particles entering in some initial state φ and coming out in some final state χ. Both are to be described in terms of our base states. To be precise, we associated the (complex) coefficients C₁ and C₂ with |φ〉 and D₁ and D₂ with |χ〉. However, the χ state is a final state, so we have to write it as 〈χ| = |χ〉† (read: chi dagger). The dagger symbol tells us we need to take the conjugate transpose of |χ〉, so the column vector becomes a row vector, and its coefficients are the complex conjugate of D₁ and D₂, which we denote as D₁* and D₂*. We combined this with Dirac’s bra-ket notation for the amplitude to go from one base state to another, as a function in time (or a function of time, I should say):

U_ij(t + Δt, t) = 〈i|U(t + Δt, t)|j〉

This allowed us to write the following matrix equation:

To see what it means, you should write it all out:

〈χ|U(t + Δt, t)|φ〉 = D₁*·(U₁₁(t + Δt, t)·C₁ + U₁₂(t + Δt, t)·C₂) + D₂*·(U₂₁(t + Δt, t)·C₁ + U₂₂(t + Δt, t)·C₂)

= D₁*·U₁₁(t + Δt, t)·C₁ + D₁*·U₁₂(t + Δt, t)·C₂ + D₂*·U₂₁(t + Δt, t)·C₁ + D₂*·U₂₂(t + Δt, t)·C₂

It’s a horrendous expression, but it’s a complex-valued amplitude or, quite simply, a complex number. So this is not nonsensical. We can now take the next step, and that’s to go from those U_ij amplitudes to the H_ij amplitudes of the Hamiltonian matrix. The key is to consider the following: if Δt goes to zero, nothing happens, so we write: U_ij = 〈i|U|j〉 → 〈i|j〉 = δ_ij for Δt → 0, with δ_ij = 1 if i = j, and δ_ij = 0 if i ≠ j. We then assume that, for small t, those U_ij amplitudes should differ from δ_ij (i.e. from 1 or 0) by amounts that are proportional to Δt. So we write:

U_ij(t + Δt, t) = δ_ij + ΔU_ij(t + Δt, t) = δ_ij + K_ij(t)·Δt

We then equated those K_ij(t) factors with − (i/ħ)·H_ij(t), and we were done: U_ij(t + Δt, t) = δ_ij − (i/ħ)·H_ij(t)·Δt. […] Well… I show you how we get those differential equations in a moment. Let’s pause here for a while to see what’s going on really. You’ll probably remember how one can mathematically ‘construct’ the complex exponential e^iθ by using the linear approximation e^iε = 1 + iε near θ = 0 and for infinitesimally small values of ε. In case you forgot, we basically used the definition of the derivative of the real exponential e^ε for ε going to zero:

So we’ve got something similar here for U₁₁(t + Δt, t) = 1 − i·[H₁₁(t)/ħ]·Δt and U₂₂(t + Δt, t) = 1 − i·[H₂₂(t)/ħ]·Δt. Just replace the ε in e^iε = 1 + iε by ε = − (E₀/ħ)·Δt. Indeed, we know that H₁₁ = H₂₂ = E₀, and E₀/ħ is, of course, just the energy measured in (reduced) Planck units, i.e. in its natural unit. Hence, if our ammonia molecule is in one of the two base states, we start at θ = 0 and then we just start moving on the unit circle, clockwise, because of the minus sign in e^−iθ. Let’s write it out:

U₁₁(t + Δt, t) = 1 − i·[H₁₁(t)/ħ]·Δt = 1 − i·[E₀/ħ]·Δt and

U₂₂(t + Δt, t) = 1 − i·[H₂₂(t)/ħ]·Δt = 1 − i·[E₀/ħ]·Δt

But what about U₁₂ and U₂₁? Is there a similar interpretation? Let’s write those equations down and think about them:

U₁₂(t + Δt, t) = 0 − i·[H₁₂(t)/ħ]·Δt = 0 + i·[A/ħ]·Δt and

U₂₁(t + Δt, t) = 0 − i·[H₂₁(t)/ħ]·Δt = 0 + i·[A/ħ]·Δt

We can visualize this as follows:

Let’s remind ourselves of the definition of the derivative of a function by looking at the illustration below: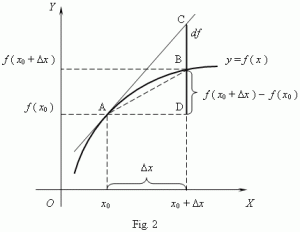The f(x₀) value in this illustration corresponds to the U_ij(t, t), obviously. So now things make somewhat more sense: U₁₁(t, t) = U₁₁(t, t) = 1, obviously, and U₁₂(t, t) = U₂₁(t, t) = 0. We then add the ΔU_ij(t + Δt, t) to U_ij(t, t). Hence, we can, and probably should, think of those K_ij(t) coefficients as the derivative of the U_ij(t, t) functions with respect to time. So we can write something like this:

These derivatives are pure imaginary numbers. That does not mean that the U_ij(t + Δt, t) functions are purely imaginary: U₁₁(t + Δt, t) and U₂₂(t + Δt, t) can be approximated by 1 − i·[E₀/ħ]·Δt for small Δt, so they do have a real part. In contrast, U₁₂(t + Δt, t) and U₂₁(t + Δt, t) are, effectively, purely imaginary (for small Δt, that is).

I can’t help thinking these formulas reflect a deep and beautiful geometry, but its meaning escapes me so far. 😦 When everything is said and done, none of the reflections above makes things somewhat more intuitive: these wavefunctions remain as mysterious as ever.

I keep staring at those P₁(t) and P₂(t) functions, and the C₁(t) and C₂(t) functions that ‘generate’ them, so to speak. They’re not independent, obviously. In fact, they’re exactly the same, except for a phase difference, which corresponds to the phase difference between the sine and cosine. So it’s all one reality, really: all can be described in one single functional form, so to speak. I hope things become more obvious as I move forward.

Post scriptum: I promised I’d show you how to get those differential equations but… Well… I’ve done that in other posts, so I’ll refer you to one of those. Sorry for not repeating myself. 🙂