Note: I have published a paper that is very coherent and fully explains what the idea of a photon might be. There is nothing stringy. Check it out: The Meaning of the Fine-Structure Constant. No ambiguity. No hocus-pocus.
Jean Louis Van Belle, 23 December 2018
Original post:
In my previous posts, I’ve been playing with… Well… At the very least, a new didactic approach to understanding the quantum-mechanical wavefunction. I just boldly assumed the matter-wave is a gravitational wave. I did so by associating its components with the dimension of gravitational field strength: newton per kg, which is the dimension of acceleration (N/kg = m/s2). Why? When you remember the physical dimension of the electromagnetic field is N/C (force per unit charge), then that’s kinda logical, right? 🙂 The math is beautiful. Key consequences include the following:
- Schrodinger’s equation becomes an energy diffusion equation.
- Energy densities give us probabilities.
- The elementary wavefunction for the electron gives us the electron radius.
- Spin angular momentum can be interpreted as reflecting the right- or left-handedness of the wavefunction.
- Finally, the mysterious boson-fermion dichotomy is no longer “deep down in relativistic quantum mechanics”, as Feynman famously put it.
It’s all great. Every day brings something new. 🙂 Today I want to focus on our weird electron model and how we get God’s number (aka the fine-structure constant) out of it. Let’s recall the basics of it. We had the elementary wavefunction:
ψ = a·e−i[E·t − p∙x]/ħ = a·e−i[E·t − p∙x]/ħ = a·cos(p∙x/ħ − E∙t/ħ) + i·a·sin(p∙x/ħ − E∙t/ħ)
In one-dimensional space (think of a particle traveling along some line), the vectors (p and x) become scalars, and so we simply write:
ψ = a·e−i[E·t − p∙x]/ħ = a·e−i[E·t − p∙x]/ħ = a·cos(p∙x/ħ − E∙t/ħ) + i·a·sin(p∙x/ħ − E∙t/ħ)
This wavefunction comes with constant probabilities |ψ|2 = a2, so we need to define a space outside of which ψ = 0. Think of the particle-in-a-box model. This is obvious oscillations pack energy, and the energy of our particle is finite. Hence, each particle – be it a photon or an electron – will pack a finite number of oscillations. It will, therefore, occupy a finite amount of space. Mathematically, this corresponds to the normalization condition: all probabilities have to add up to one, as illustrated below. Now, all oscillations of the elementary wavefunction have the same amplitude: a. [Terminology is a bit confusing here because we use the term amplitude to refer to two very different things here: we may say a is the amplitude of the (probability) amplitude ψ. So how many oscillations do we have? What is the size of our box? Let us assume our particle is an electron, and we will reduce its motion to a one-dimensional motion only: we’re thinking of it as traveling along the x-axis. We can then use the y- and z-axes as mathematical axes only: they will show us how the magnitude and direction of the real and imaginary component of ψ. The animation below (for which I have to credit Wikipedia) shows how it looks like.
Now, all oscillations of the elementary wavefunction have the same amplitude: a. [Terminology is a bit confusing here because we use the term amplitude to refer to two very different things here: we may say a is the amplitude of the (probability) amplitude ψ. So how many oscillations do we have? What is the size of our box? Let us assume our particle is an electron, and we will reduce its motion to a one-dimensional motion only: we’re thinking of it as traveling along the x-axis. We can then use the y- and z-axes as mathematical axes only: they will show us how the magnitude and direction of the real and imaginary component of ψ. The animation below (for which I have to credit Wikipedia) shows how it looks like. Of course, we can have right- as well as left-handed particle waves because, while time physically goes by in one direction only (we can’t reverse time), we can count it in two directions: 1, 2, 3, etcetera or −1, −2, −3, etcetera. In the latter case, think of time ticking away. 🙂 Of course, in our physical interpretation of the wavefunction, this should explain the (spin) angular momentum of the electron, which is – for some mysterious reason that we now understand 🙂 – always equal to J = ± ħ/2.
Of course, we can have right- as well as left-handed particle waves because, while time physically goes by in one direction only (we can’t reverse time), we can count it in two directions: 1, 2, 3, etcetera or −1, −2, −3, etcetera. In the latter case, think of time ticking away. 🙂 Of course, in our physical interpretation of the wavefunction, this should explain the (spin) angular momentum of the electron, which is – for some mysterious reason that we now understand 🙂 – always equal to J = ± ħ/2.
Now, because a is some constant here, we may think of our box as a cylinder along the x-axis. Now, the rest mass of an electron is about 0.510 MeV, so that’s around 8.19×10−14 N∙m, so it will pack some 1.24×1020 oscillations per second. So how long is our cylinder here? To answer that question, we need to calculate the phase velocity of our wave. We’ll come back to that in a moment. Just note how this compares to a photon: the energy of a photon will typically be a few electronvolt only (1 eV ≈ 1.6 ×10−19 N·m) and, therefore, it will pack like 1015 oscillations per second, so that’s a density (in time) that is about 100,000 times less.
Back to the angular momentum. The classical formula for it is L = I·ω, so that’s angular frequency times angular mass. What’s the angular velocity here? That’s easy: ω = E/ħ. What’s the angular mass? If we think of our particle as a tiny cylinder, we may use the formula for its angular mass: I = m·r2/2. We have m: that’s the electron mass, right? Right? So what is r? That should be the magnitude of the rotating vector, right? So that’s a. Of course, the mass-energy equivalence relation tells us that E = mc2, so we can write:
L = I·ω = (m·r2/2)·(E/ħ) = (1/2)·a2·m·(mc2/ħ) = (1/2)·a2·m2·c2/ħ
Does it make sense? Maybe. Maybe not. You can check the physical dimensions on both sides of the equation, and that works out: we do get something that is expressed in N·m·s, so that’s action or angular momentum units. Now, we know L must be equal to J = ± ħ/2. [As mentioned above, the plus or minus sign depends on the left- or right-handedness of our wavefunction, so don’t worry about that.] How do we know that? Because of the Stern-Gerlach experiment, which has been repeated a zillion times, if not more. Now, if L = J, then we get the following equation for a: 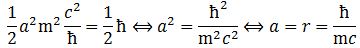 This is the formula for the radius of an electron. To be precise, it is the Compton scattering radius, so that’s the effective radius of an electron as determined by scattering experiments. You can calculate it: it is about 3.8616×10−13 m, so that’s the picometer scale, as we would expect.
This is the formula for the radius of an electron. To be precise, it is the Compton scattering radius, so that’s the effective radius of an electron as determined by scattering experiments. You can calculate it: it is about 3.8616×10−13 m, so that’s the picometer scale, as we would expect.
This is a rather spectacular result. As far as I am concerned, it is spectacular enough for me to actually believe my interpretation of the wavefunction makes sense.
Let us now try to think about the length of our cylinder once again. The period of our wave is equal to T = 1/f = 1/(ω/2π) = 1/[(E/ħ)·2π] = 1/(E/h) = h/E. Now, the phase velocity (vp) will be given by:
vp = λ·f = (2π/k)·(ω/2π) = ω/k = (E/ħ)/(p/ħ) = E/p = E/(m·vg) = (m·c2)/(m·vg) = c2/vg
This is very interesting, because it establishes an inverse proportionality between the group and the phase velocity of our wave, with c2 as the coefficient of inverse proportionality. In fact, this equation looks better if we write as vp·vg = c2. Of course, the group velocity (vg) is the classical velocity of our electron. This equation shows us the idea of an electron at rest doesn’t make sense: if vg = 0, then vp times zero must equal c2, which cannot be the case: electrons must move in space. More generally, speaking, matter-particles must move in space, with the photon as our limiting case: it moves at the speed of light. Hence, for a photon, we find that vp = vg = E/p = c.
How can we calculate the length of a photon or an electron? It is an interesting question. The mentioned orders or magnitude of the frequency (1015 or 1020) gives us the number of oscillations per second. But how many do we have in one photon, or in one electron?
Let’s first think about photons, because we have more clues here. Photons are emitted by atomic oscillators: atoms going from one state (energy level) to another. We know how to calculate to calculate the Q of these atomic oscillators (see, for example, Feynman I-32-3): it is of the order of 108, which means the wave train will last about 10–8 seconds (to be precise, that is the time it takes for the radiation to die out by a factor 1/e). Now, the frequency of sodium light, for example, is 0.5×1015 oscillations per second, and the decay time is about 3.2×10–8 seconds, so that makes for (0.5×1015)·(3.2×10–8) = 16 million oscillations. Now, the wavelength is 600 nanometer (600×10–9) m), so that gives us a wavetrain with a length of (600×10–9)·(16×106) = 9.6 m.
These oscillations may or may not have the same amplitude and, hence, each of these oscillations may pack a different amount of energies. However, if the total energy of our sodium light photon (i.e. about 2 eV ≈ 3.3×10–19 J) are to be packed in those oscillations, then each oscillation would pack about 2×10–26 J, on average, that is. We speculated in other posts on how we might imagine the actual wave pulse that atoms emit when going from one energy state to another, so we don’t do that again here. However, the following illustration of the decay of a transient signal dies out may be useful.
This calculation is interesting. It also gives us an interesting paradox: if a photon is a pointlike particle, how can we say its length is like 10 meter or more? Relativity theory saves us here. We need to distinguish the reference frame of the photon – riding along the wave as it is being emitted, so to speak – and our stationary reference frame, which is that of the emitting atom. Now, because the photon travels at the speed of light, relativistic length contraction will make it look like a pointlike particle.
What about the electron? Can we use similar assumptions? For the photon, we can use the decay time to calculate the effective number of oscillations. What can we use for an electron? We will need to make some assumption about the phase velocity or, what amounts to the same, the group velocity of the particle. What formulas can we use? The p = m·v is the relativistically correct formula for the momentum of an object if m = mv, so that’s the same m we use in the E = mc2 formula. Of course, v here is, obviously, the group velocity (vg), so that’s the classical velocity of our particle. Hence, we can write:
p = m·vg = (E/c2)·vg ⇔ vg = p/m = p·c2/E
This is just another way of writing that vg = c2/vp or vp = c2/vg so it doesn’t help, does it? Maybe. Maybe not. Let us substitute in our formula for the wavelength:
λ = vp/f = vp·T = vp⋅(h/E) = (c2/vg)·(h/E) = h/(m·vg) = h/p
This gives us the other de Broglie relation: λ = h/p. This doesn’t help us much, although it is interesting to think about it. The f = E/h relation is somewhat intuitive: higher energy, higher frequency. In contrast, what the λ = h/p relation tells us that we get an infinite wavelength if the momentum becomes really small. What does this tell us? I am not sure. Frankly, I’ve look at the second de Broglie relation like a zillion times now, and I think it’s rubbish. It’s meant to be used for the group velocity, I feel. I am saying that because we get a non-sensical energy formula out of it. Look at this:
- E = h·f and p = h/λ. Therefore, f = E/h and λ = p/h.
- v = f·λ = (E/h)∙(p/h) = E/p
- p = m·v. Therefore, E = v·p = m·v2
E = m·v2? This formula is only correct if v = c, in which case it becomes the E = mc2 equation. So it then describes a photon, or a massless matter-particle which… Well… That’s a contradictio in terminis. 🙂 In all other cases, we get nonsense.
Let’s try something differently. If our particle is at rest, then p = 0 and the p·x/ħ term in our wavefunction vanishes, so it’s just:
ψ = a·e−i·E·t/ħ = a·cos(E∙t/ħ) − i·a·sin(E∙t/ħ)
Hence, our wave doesn’t travel. It has the same amplitude at every point in space at any point in time. Both the phase and group velocity become meaningless concepts. The amplitude varies – because of the sine and cosine – but the probability remains the same: |ψ|2 = a2. Hmm… So we need to find another way to define the size of our box. One of the formulas I jotted down in my paper in which I analyze the wavefunction as a gravitational wave was this one: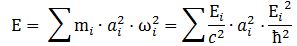
It was a physical normalization condition: the energy contributions of the waves that make up a wave packet need to add up to the total energy of our wave. Of course, for our elementary wavefunction here, the subscripts vanish and so the formula reduces to E = (E/c2)·a2·(E2/ħ2), out of which we get our formula for the scattering radius: a = ħ/mc. Now how do we pack that energy in our cylinder? Assuming that energy is distributed uniformly, we’re tempted to write something like E = a2·l or, looking at the geometry of the situation:
E = π·a2·l ⇔ l = E/(π·a2)
It’s just the formula for the volume of a cylinder. Using the value we got for the Compton scattering radius (a = 3.8616×10−13 m), we find an l that’s equal to (8.19×10−14)/(π·14.9×10−26) =≈ 0.175×1012… Meter? Yes. We get the following formula:

0.175×1012 m is 175 million kilometer. That’s – literally – astronomic. It corresponds to 583 light-seconds, or 9.7 light-minutes. So that’s about 1.17 times the (average) distance between the Sun and the Earth. You can see that we do need to build a wave packet: that space is a bit too large to look for an electron, right? 🙂
Could we possibly get some less astronomic proportions? What if we impose that l should equal a? We get the following condition: We find that m would have to be equal to m ≈ 1.11×10−36 kg. That’s tiny. In fact, it’s equivalent to an energy of about equivalent to 0.623 eV (which you’ll see written as 623 milli-eV. This corresponds to light with a wavelength of about 2 micro-meter (μm), so that’s in the infrared spectrum. It’s a funny formula: we find, basically, that the l/a ratio is proportional to m4. Hmm… What should we think of this? If you have any ideas, let me know !
We find that m would have to be equal to m ≈ 1.11×10−36 kg. That’s tiny. In fact, it’s equivalent to an energy of about equivalent to 0.623 eV (which you’ll see written as 623 milli-eV. This corresponds to light with a wavelength of about 2 micro-meter (μm), so that’s in the infrared spectrum. It’s a funny formula: we find, basically, that the l/a ratio is proportional to m4. Hmm… What should we think of this? If you have any ideas, let me know !
Post scriptum (3 October 2017): The paper is going well. Getting lots of downloads, and the views on my blog are picking up too. But I have been vicious. Substituting B for (1/c)∙i∙E or for −(1/c)∙i∙E implies a very specific choice of reference frame. The imaginary unit is a two-dimensional concept: it only makes sense when giving it a plane view. Literally. Indeed, my formulas assume the i (or −i) plane is perpendicular to the direction of propagation of the elementary quantum-mechanical wavefunction. So… Yes. The need for rotation matrices is obvious. But my physical interpretation of the wavefunction stands. 🙂

I like your idea that the reduced Compton wavelength is the scattering radius of the electron. I’ve included this idea in a derivation for the spectral lines of hydrogen. the link follows
Click to access Hydrogen.pdf